1. Introduction
Traditionally, information security needed encryption, authentication, key management, non-repudiation and authorization which were being met using several techniques. Standardization of algorithms by National Institute of Standards and Technology (NIST) has facilitated international communication for banking and information transfer using these standards. Encryption can be carried out using Advanced Encryption Standard (AES) using variable block lengths (128, 192 or 256 bits) and variable key lengths (128, 192 or 256 bits). Solutions for light weight applications such as those for Internet of Things (IoT) are also being standardized. Message integrity is possible using host of hash algorithms such as SHA-1, SHA-2 etc., and more recently using SHA-3 algorithm. Authentication is possible using well known Rivest-Shamir-Adleman (RSA) algorithm needing 2048/4096 bit operations. Elliptic Curve Cryptography (ECC) is also quite popular and used in several practical systems such as WhatsApp, Blackberry etc. Key exchange is possible using Diffie-Hellman algorithm and its variations. Digital Signatures can be carried out using RSA algorithm or Elliptic Curve Digital Signature Algorithm (ECDSA) or DSA (Digital Signature Algorithm). All these algorithms derive security from difficulty in solving some mathematical problems such as factorization problem or discrete logarithm problem. Though published literature gives evidence of solving factorization problem upto 768 bits only, it is believed that using Quantum computers, these problems could be solved by the end of this decade. This is due to availability of the pioneering work of Shor and Grover [1]. For factoring an integer of N bits, Shor’s algorithm takes 
quantum gates. As such, there is ever growing interest in being ready for the next decade with algorithms that may resist attacks in the quantum computer era. NIST has foreseen this need and has invited proposals from researchers all over the world. In the first round, about 66 submissions were received which have been scrutinized for completeness of submissions , novelty of the approach and security and 25 of these were promote to second round to improve based on the comments received on the first round submission. These will be analyzed for security and some will be selected for final recommendation for use by industry. These are for encryption/decryption, key agreement, hashing and Digital Signatures for both hardware and software implementations. In this paper, we present a brief survey of the state of the art in post-Quantum Cryptography (PQC) followed by study of one of technique referred to as Learning With Errors (LWE) in some detail.
There are five areas into which PQC algorithms can be classified. These are as follows:
|
Public Key Encryption(PKE) Key Encapsulation Mechanism (KEM) |
|
|
Code based |
Lattice based |
|
BIKE |
CRYSTALS – KYBER |
|
Classic McEliece |
Frodo KEM |
|
HQC |
LAC |
|
LEDAcrypt (merger of LEDAkem/LEDApkc) |
New Hope |
|
NTS-KEM |
NTRU (merger of NTRU Encrypt/NTRU-HRSS-KEM) |
|
ROLLO (merger of LAKE/LOCKER/Ouroboros-R) |
NTRU Prime |
|
RQC Codebased |
Round5 (merger of Hila5/Round2) |
|
|
SABER |
|
|
Three Bears |
|
Key Exchange supersingular Elliptic curve |
|
SIKE |
|
Digital Signatures |
||
|
Lattice based |
Hash based |
Multivariate |
|
CRYSTALS-DILITHIUM |
SPHINCS
|
GeMSS |
|
FALCON |
|
LUOV |
|
qTESLA |
|
MQDSS |
|
|
|
Rainbow |
Table I. Second round submissions of PQC competition of NIST
In this article, we focus on Ring – LWE (Ring – Learning with errors) based Encryption, Key exchange and KEM operations using one of the PQC entries referred to as New Hope.
This is based on the difficulty of finding a solution for the shortest vector problem in a lattice. Given a number of independent vectors b1, b2,.., bn, the lattice is defined as 
for all ai belonging to set Z. The set 
is called a basis of the lattice.
We first describe integer mode LWE and then we deal with Ring-LWE. Initially we create a secret key value (s) and another value (e) and choose a prime p. Next we select a number of values (A[ ]) and calculate B[ ] = A[ ] × s + e. The values of A[ ] and B[ ] become our public key. If s is a single value, A and B are one dimensional matrices. Note that e is error column matrix. The difficult problem to be solved is given A and B, finding s. This is called search problem. Given enough samples, can we find the secret? On the other hand, there is another problem-decision-can we distinguish a random sample and m independent samples of LWE. The decision problem aims to find whether there is a secret in the samples. Note that without the error vector e (i.e. e = 0), we can easily solve the system of linear equations. In the presence of errors with some distribution say discrete Gaussian distribution (mean zero and standard deviation σ), solving the system is believed to be quantum hard. Note that error distribution in fact hides the characteristic of the plain text. Consider an example of small dimensions with chosen prime p =13:
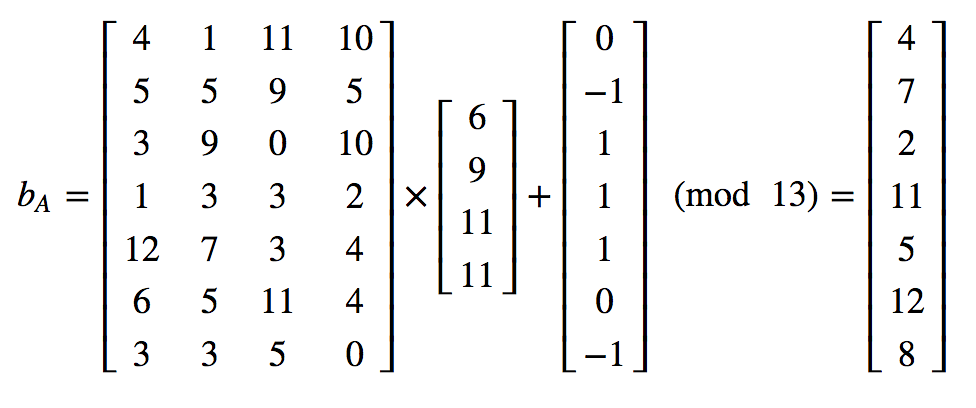
We next consider LWE in a polynomial ring. In this technique, A, s and B are n– th degree polynomials given as
Note that all operations are modulo (xn+1). This means that when we multiply two polynomials, the degree will be (2n-2) and this result needs to be reduced mod (xn+1). This is simple by noting that x4 = -1, x5 = –x etc. Note also that the polynomials coefficients are multiplied mod q, where q is a chosen prime. Evidently all coefficients will be less than q. We next consider an example with q=13.
We compute (A x s) first and reduce mod (x4+1).
|
|
|
|
10 |
11 |
1 |
4 |
|
|
|
|
11 |
11 |
9 |
6 |
|
|
|
|
60 |
66 |
6 |
24 |
|
|
|
90 |
99 |
9 |
36 |
-90 |
|
|
110 |
121 |
11 |
44 |
-110 |
-121 |
|
110 |
121 |
11 |
44 |
-110 |
-121 |
-11 |
|
|
|
|
214 |
9 |
-189 |
-189 |
|
|
|
e |
1 |
1 |
-1 |
0 |
|
|
|
Mod13 |
7 |
10 |
5 |
10 |
Finally, we get from the last row, the result polynomial as 
.
Evidently n2 modulo multiplications and addition of all these products together with e mod q is required.
We next consider Key exchange using RWE which is similar to Diffie-Hellman Key exchange. We use subscripts A and B to indicate their respective parameters. We consider Alice and Bob as the two sharing the key and describe the steps involved.
Note that all the computation is done in ring of polynomials. Since Alice and Bob use different error vectors, the shared keys will have different rounding errors. This can be resolved by using a process called ‘reconciliation’. In this method, one user sends a hint to the other and both Alice and Bob can use the hint to arrive at the correct shared key.
We next describe how a message can be encrypted. We generate 20 random numbers for our public key A. We also generate an error vector e of 20 samples and we choose a prime q = 97. We also choose a secret key s = 5.
A = [80, 86, 19, 62, 2, 83, 25, 47, 20, 58, 45, 15, 30, 68, 4, 13, 8, 6, 42, 92]
e = [3, 3, 4, 1, 3, 3, 4, 4, 1, 4, 3, 3, 2, 2, 3, 2, 4, 4, 1, 3]
Next we compute B = (A. s + e) mod q as shown below:
B = [15, 45, 2, 20, 13, 30, 32, 45, 4, 3, 34, 78, 55, 51, 23, 67, 44, 34, 17, 75]
Not that B is also public key. Now we can distribute lists A and B to anyone. Suppose we want to encrypt a message bit m.
We pick from our lists A and B few samples and compute u and v as follows:
u=∑(Asamples)(mod q) and v=∑(Bsamples) + (q/2)m(mod q)
The encrypted message is (u, v). To decrypt, we calculate:
Dec = v−su(mod q)
If Dec is less than q/2, the message is a zero, else it is a 1.
For our example we choose from A and B the entries in the five locations [18, 5, 8, 13, 11] and compute u and v as u=34 and v = 83. The encrypted message is (34, 83). We get Dec = (83 -5 × 34) mod 97 = 10. Since Dec is less than q/2, we get m = 0. The reader may note however that just for sending one bit we have to transmit two number of size q.
In practice R-LWE encryption has three steps: Key generation, Encryption and Decryption.These are as follows:
KeyGen (a): Choose two polynomials r1 and r2 and compute p = r1 – ar2.The public key is (a, p) and private key is r2.the polynomial r1 is noise and is no longer required after key generation.
Encrypt (a, p, m): The message m is encoded as a polynomial m′ in the ring. Three polynomials e1, e2 and e3 are sampled from a distribution. Compute c1 = ae1+ e2 and c2 = pe1+ e3 + m′. The final cipher text is (c1, c2).
Dec(c1,c2,r2): Compute m′ = c1r2 + c2 and recover the original message.
The message is encoded first by writing 1 as (q-1)/2 and retaining ‘0’ as ‘0’. The decoding is done by following the rule:
if (q-1)/4 ≤ m′ ≤ 3(q-1)/4, return 1, otherwise return 0. Note that e1, e2, e3 will not affect the decrypted text if a, q, e, r1 and r2 are properly chosen.
Four primitives will be needed in the implementation: (a) Discrete Gaussian sampler (b) Polynomial multiplier (c) countermeasures against side channel attacks (d) True Random number generator. Different approaches may be used in different algorithms regarding these four aspects. We consider for illustration New Hope next.
With the above background, we describe briefly New Hope Key Encapsulation Mechanism (KEM) and public key encryption (PKE) which uses lot of steps in the generation of A, s and e for meeting the security requirements. Two versions of New hope one with N = 512 and another with 1024 are available. The prime q chosen for N=1024 is 12259. Evidently this means that all coefficients in the 1024 degree polynomials are of 14 bit length. Now the reader may get an idea of the key length needed. The Table II gives the parameters recommended. CPA and CCA mean Chosen Plain Text attacks and Chosen Cipher Text attacks.
|
Table II. Parameter sets for New Hope KEM for CPA and CCA. |
|||
|
Parameter set |
|
|
|
|
New Hope512-CPA-KEM |
928 |
869 |
1088 |
|
New Hope1024-CPA-KEM |
1824 |
1792 |
2176 |
|
New Hope 512-CCA-KEM |
928 |
1888 |
1120 |
|
New Hope 512-CCA-KEM |
1824 |
3680 |
2208 |
Table II: Two versions of New hope one with N = 512 and
another with 1024 are available as shown.
|
Parameters q = 12289 < 214, n = 1024 Error distribution: ψ16 |
||
|
Alice (Server) |
|
Bob(client) |
|
$ seed ← {0,1}256 |
|
|
|
a←Parse(SHAKE-128(seed)) |
|
|
|
$ s,e ← ψn16 |
|
$ s′,e′,e′′ ← ψn16 |
|
b←as+e |
(b,seed)
|
a←Parse(SHAKE-128(seed)) |
|
|
|
u←as′+e′′ |
|
|
|
v←bs′+e′′ |
|
v′←us |
(u,r) ← |
$ r ← HelpRec(v) |
|
ν←Rec(v′,r) |
|
ν←Rec(v,r) |
|
μ←SHA3-256(ν) |
|
μ←SHA3-256(ν) |
Figure 1: New Hope Algorithm in simplified form
In the above code, the symbol ψ stands for distributions from which the coefficients of various polynomials are taken. The HelpRec step helps for reconciliation so that both the users arrive at the same key. The parameter μ indicates the final key obtained by hashing v. Since the polynomials are of degree 1024, multiplication in the ring with coefficients reduced mod q is a complex process. This can be solved by using Number Theoretic Transforms (NTT). Both the polynomials A and B to be multiplied mod (xn+1) are transformed using NTT and the resulting 1024 values can be multiplied point-wise and inverse NTT can be applied to get the actual product. This needs initial transformation of the polynomial coefficients of A and B using a primitive root ω defined as ωN = 1mod p. As an illustration, for N = 1024, p = 12277, we have ω = 49. Note that New Hope uses SHAKE256 hash function (SHA3 variation) for various functions, which takes a seed of 256 bits and outputs several bytes as desired.
Post Quantum Cryptographic (PQC) algorithms are more difficult to understand than conventional cryptographic algorithms like AES, RSA etc. It may be noted that while quantum computers need different environment, PQC algorithms will still be implemented in FPGAs, GPUs and embed processors and ASICs. Attempts also have been made to incorporate suite of PQC algorithms in Web browsers and other applications and even in IoT devices with limited resources.
[1] P. Shor, Algorithms for Quantum computation: Discrete logarithms and Factoring, Foundations of Computer Science, 1994 Proceedings, 35th Annual Symposium, pp.124-134, Nov.1994.
[2] V. Lyubashevsky, C. Piekert and O. Regev, On ideal lattices and Learning with Errors over Rings, Cryptology ePrint Archive, Report 2012/230, 2012.
[3] S.S. Roy, F. Vercauteren and I. Verbauwhede, High precision Discrete Gaussian sampling on FPGAs, Selected Areas in Cryptology-SAC 2013, pp 383-401, 2014.
[4] S.S. Roy, F.Vercauteren, N.Mentens, D.D.Chen and I. Verbauwhede, Compact Ring LWE cryptoprocessor, Cryptographic Hardware and Embedded Systems, CHES 2014, Vol 8731, pp 371-391.
[5] A. Mariano et al., A practical view of the state-of-the-art of Lattice-based Cryptanalysis, IEEE Access, Vol5, pp 24184-24202, 2017.
[6] D. Liu et al. A resource-efficient and side-channel secure Hardware implementation of Ring-LWE cryptographic processor, IEEE Transactions on Circuits and Systems-I, Regular Papers, Vol.66, pp 1474-1483, 2019.
[7] E. Alkim, L.Ducas, T.Poppelmann and P.Scwabe, Post-Quantum Key Exchange – a New Hope, https://eprint.iacr.org/2015/1092.
[8] E. Alkim et al, New Hope: Algorithm Specification and syupporting Documentation, NIST, Post Quantum Cryptography web site, Round 2 submissions, pp 1-46, 2019.
[9] Bill Buchanan, Learning with Errors and Ring learning with Errors, https://medium.com/a security site-wghen-bob-meets Alice, 2019
