A thing is symmetrical if there is something we can do to it so that after we have done it, it looks the same as it did before. If you rotate a perfect and rigid sphere or even as it is rotating about any axis through its center, you will not know that it is rotating by seeing it with your unaided
eyes. To mathematician and physicists, symmetry is invariance under transformations. That is, the end state looks the same after the transformation T as the start state. It means f(x) = f(y = T(x)) = f(y). The transformation only changes the symbols defining the function f but not
its form.
Here is an example: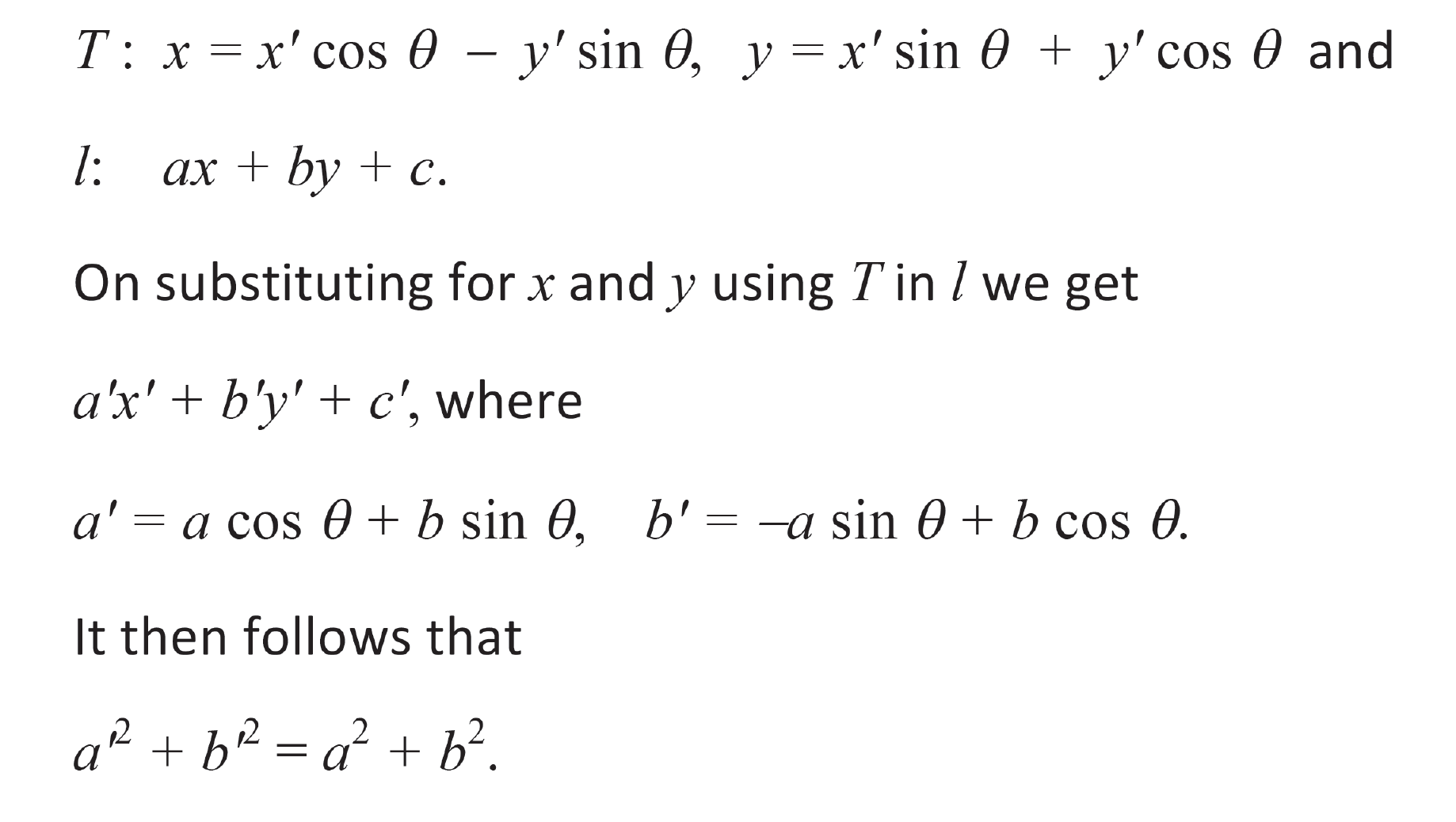
Accordingly, a2 + b2 is called an invariant of l under every
transformation of the type T.
Here is a breathtaking example summarized in Figure 1.
Maxwell’s equations contain two constants, 
and 
, which may be determined experimentally. The constant is the same no matter what we choose for our unit of charge. Experiments showed that is the square of the velocity of propagation of electromagnetic influences. Using available data, Maxwell obtained 
= 310,740,000 meters/second. It was not obvious that the coefficient c in Maxwell’s equations was also the speed of light propagation but Maxwell did notice the mysterious coincidence, and remarked in 1865:
This velocity is so nearly that of light, that it seems we have strong reason to conclude that light itself (including radiant heat, and other radiations if any) is an electromagnetic disturbance in the form of waves propagated through the electromagnetic field according to electromagnetic laws.
Numerous experiments have proved Maxwell correct even at the level of quantum mechanics.
An inertial reference frame is a coordinate system which moves with constant velocity, i.e., its movement is given by the Galilean transformation
where r0 and t0 represent respective shifts in the origin of space and time, and v is the relative velocity of the two inertial reference frames (marked with and without a prime), the time between two events (t2 − t1) is the same for all inertial reference frames and the distance between two simultaneous events (or, equivalently, the length of any object, |r2 – r1|) is also the same.
Maxwell’s equations were met with skepticism since they were not invariant with respect to the Galilean transformation. It was believed at the time that any law of nature should be so invariant. However, experiment after experiment failed to find a flaw in Maxwell’s equations.
Later when Lorentz showed that Maxwell’s equations are invariant under the transformation
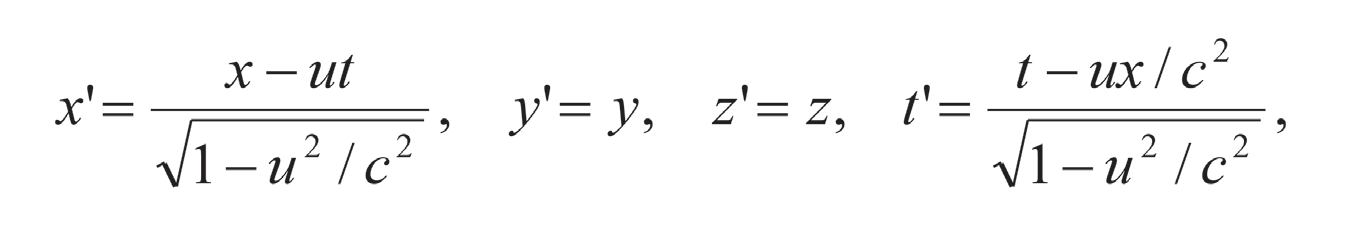
where, for simplicity, shifts in origin have been ignored, and the relative velocity is assumed to be in the -direction. Under the Lorentz transformation, time and distance between events may differ among inertial reference frames; however, the Lorentz scalar distance s2 between two events is the same in all inertial reference frames
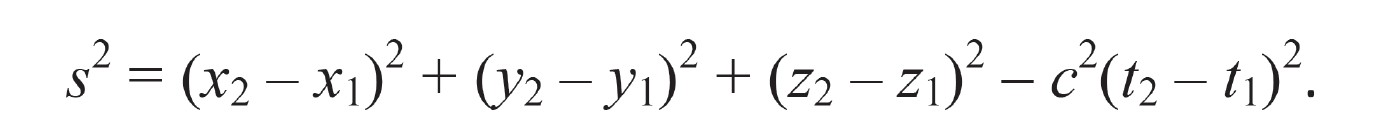
In this reference frame, c is only coincidently the speed of light; fundamentally it is a property of space-time, a conversion factor between time units and length units.
Here is the amazing symmetry. The principle of relativity may be stated as follows: Any process in nature occurs in the same manner in any inertial reference frame; in all inertial frames a law has the same form.
Drawing on the very essence of the relativity principle Einstein postulated that the velocity of light in a vacuum must be the same in all inertial reference frames. This was a remarkable breakthrough in science since it spectacularly changed our notions of space and time. It was the study of the relativity problem that concentrated physicist’s attention most sharply on symmetry in physical laws. It led Eugene P. Wigner (1960) to make, in amazement, the often quoted statement,
It led another famous physicist, Richard P. Feynman, to comment,
Eugene P. Wigner won the Nobel Prize in physis in 1963, Richard Feynman won the Nobel Prize in Physics in 1965.
An intimate relationship between conservation and symmetry was found by Emmy Nöther, an associate of David Hilbert, working with Felix Klein, Hilbert, and Albert Einstein on the mathematical foundations of physics and relativity proved a beautiful theorem in 1918:
If the first integral of a function of generalized coordinates and first derivatives is invariant under an infinitesimal transformation, then the first integral of the related Euler- Lagrange equation is a constant.2
It holds for all physical laws based upon the action principle. In simpler language: For every observable symmetry in Nature there is a corresponding entity that is conserved. And for every conservation law there is a corresponding symmetry.
The action is an integral quantity that is used to determine the evolution of a physical system between two defined states, say, x(t1) and x(t2), using the calculus of variations. The requirement that the action integral be stationary under small perturbations of the evolution is equivalent to a set of differential equations (called the Euler-Lagrange equations).
If we assume that the function L (the integrand of the action integral) depends only on the coordinate x() and its time derivative , and does not depend on time explicitly then the action integral can be written as
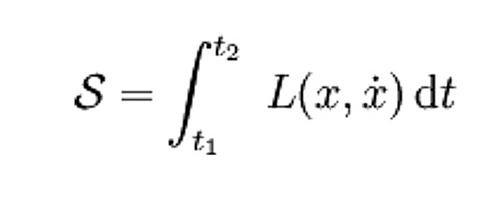
The Euler-Lagrange equation is then (from variational calculus)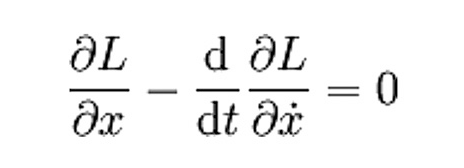
In mechanics, where is the total kinetic energy and is the total potential energy of the system.
Nöther’s theorem allows one to gain powerful insights into the laws of Nature when one analyzes transformations that leave the form of the laws invariant. The theorem is deeply tied to quantum mechanics as it identifies physical variables that are related by the Heisenberg uncertainty principle (such as position and momentum, and also time and energy) using only the principles of classical mechanics. The formal statement of the theorem derives from the condition of invariance alone, an expression for the current associated with a conserved physical quantity. The conserved quantity is called the Nöther charge and the current the Nöther current, which is defined by a divergence free vector field.
Viewed differently, it is a consequence of the invariance of the laws of physics under translations in space. In layman terms: there are no absolute positions; what matters is not where an object is in absolute terms, but where it is relative to other objects.
That is, it is a consequence of the invariance of the laws of physics under rotations in space.
That is, it is a consequence of the invariance of the laws of physics under translations in time.
What does it all imply? Inter alia, it means:
A mathematical law of physics involving the x coordinate of two objects, x1 and x2, may contain only their differences but not their absolute values. The law can have the form f(x2 — x1) = 0 but not f(x1) = 0 or f(x2) = 0. Or, even for a single object, it may contain the time derivative of its x coordinate since d(x + c)/dt is the same as dx/dt for any constant c. Such equations will remain invariant under a translation. There is one common characteristic to these transformations under which physical laws remain unchanged. Namely that all are global: the value that characterizes the transformation is the same everywhere in all of spacetime.
The three-dimensionality of space predetermines the vector nature of momentum and angular momentum, and the laws of conservation of momentum and angular momentum are vector laws. The one-dimensionality of time predetermines the scalar nature of energy and the corresponding conservation law. The relationship of conservation laws to space-time symmetry means that the passage of time or a translation and a rotation in space cannot cause a change in the physical state of the system.
The laws of momentum, angular momentum, and energy are used both in classical mechanics and in quantum mechanics. So far no experiment has shown that the laws of nature may be variant under translation in time, and under translation and rotation in space. It is interesting that Euclid’s fourth axiom (all right angles are congruent), in effect, asserts the isotropy and homogeneity of space, so that a figure in one place could have the same (i.e. congruent) geometrical shape as a figure in some other place.
The only doctoral student of Paul Gordon, Nöther in her doctoral thesis listed systems of 331 covariant (varying with another variable quantity in a manner that leaves a specified relationship unchanged) forms following Gordan’s constructive approach to the problem of algebraic invariants. After 1919, she moved on to work on ideal theory, producing an abstract theory which helped develop ring theory into a major mathematical topic.
It was said of her that she had a loud, disagreeable voice, and a mind of first-rate brilliance. One of her collaborators remarked that “she looked like an energetic and very nearsighted washerwoman.” More charitably, Hermann Weyl said in eulogy “the graces did not preside at her cradle.” Yet what she did not possess, she created when she proved the most profoundly beautiful theorem of mathematical physics3. Emmy Nöther died on 14 April 1935.
An Obituary by Einstein
In the realm of algebra, in which the most gifted mathematicians have been busy for centuries, she discovered methods which have proved of enormous importance in the development of the present-day younger generation of mathematicians.
Emmy Nöther, who, in spite of the efforts of the great Göttingen mathematician, Hilbert, never reached the academic standing due her in her own country, …. Her unselfish, significant work over a period of many years was rewarded by the new rulers of Germany with a dismissal, which cost her the means of maintaining her simple life and the opportunity to carry on her mathematical studies. Farsighted friends of science in this country [U.S.A.] were fortunately able to make such arrangements at Bryn Mawr College and at Princeton that she found in America up to the day of her death not only colleagues who esteemed her friendship but grateful pupils whose enthusiasm made her last years the happiest and perhaps the most fruitful of her entire career.
— Albert Einstein, New York Times, May 5, 1935
The law of conservation of energy had been used in mechanics before Galileo. In fact, in the late 15th century the great Leonardo da Vinci postulated the impossibility of perpetuum mobile. In his book On True and False Science he wrote: “Oh, seekers of perpetual motion, how many empty projects you have created in those searches.” The laws of conservation of linear momentum and angular momentum were formulated later, in the 17-18th centuries. It was not, however, till the beginning of the 20th century that the laws assumed prominence.
The attitude to them changed radically only after it was discovered that these laws were related to principles of invariance. Once this relation had been revealed, it became clear that conservation laws are predominant among other laws of nature.
The analog of Nöther’s theorem in quantum field theory is the Ward-Takahashi identities4, which lead to results such as the conservation of electric charge from the invariance with respect to the gauge invariance5 of the scalar electric potential and vector magnetic potential. Noether's theorem is also valid in quantum field theory.
If you look back at Maxwell’s equations in electro-magnetism in Figure. 1, Maxwell made an amazing leap of imagination in writing them. In Maxwell’s equations, the last equation, namely
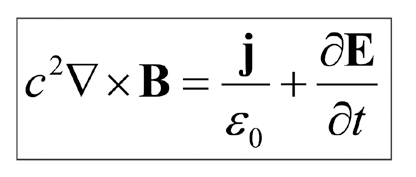
the last term 
was inspired by symmetry that Maxwell intuitively believed existed between electric and magnetic fields. The unification of electricity and magnetism was a breakthrough in classical physics. In a static world electricity and magnetism are separate phenomena. By taking the divergence of the boxed equation we can show that charge is conserved.
Lorentz transformation
Twenty years after Maxwell gave his equations, H. A. Lorentz noticed that the equations are invariant under the transformation known by his name (see Fig. 1). Note in particular that Maxwell’s equations are not invariant under the Galilean transformation. Einstein, following a suggestion originally made by Poincaré, then proposed that all the physical laws should remain invariant under a Lorentz transformation. That is, we should change, not the laws of electrodynamics, but the laws of mechanics— i.e., Newton’s laws of motion. When this change was made, it turned out that mass must change as
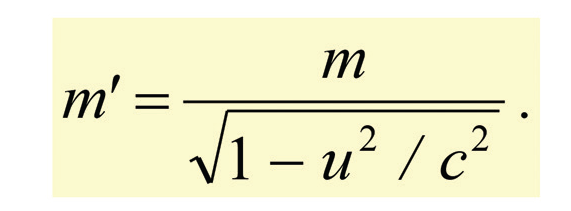
And the laws of nature are once again in harmony!6
The law of conservation of electric charge is the symmetry of physical laws with respect to changes in the magnitude of the intensity of the electric field.
The 1887 experiment of Albert A. Michelson (Nobel Prize in Physics, 1907) and Edward W. Morley to measure the speed of the Earth relative to the ether resulted in failure. The Dutch physicist Hendrik A. Lorentz (Nobel Prize in Physics, 1902) attempted to explain the failure by assuming that matter moving through ether experienced a contraction.7
In 1905, Albert Einstein (age 26) explained the null result of the experiment differently. He theorized that the Lorentz contraction was not a contraction of a moving mass but the transformation, in 4-dimensional space-time of a moving reference frame, and that the speed of light in vacuum is a constant in all inertial reference frames. This was Einstein’s special theory of relativity. In a subsequent paper, Einstein showed that not only was 4-dimensional
space-time transformed in a moving reference frame, but that mass and energy were related in a similar transformation: E = mc2.
“The electromagnetic field can also be viewed as a curvature, not the curvature of space-time but the curvature of some fictitious phase space.” — Saunders Mac Lane. Mathematics. Science, 4 July 1980, Vol. 209, pp. 104-110; 108.
(In a phase space, every degree of freedom or parameter of the system is represented as an axis of a multidimensional space. For every possible state of the system, or allowed combination of values of the system’s parameters, a point is plotted in the multidimensional space. In classical mechanics the phase space co-ordinates are the generalized coordinates qi and their conjugate generalized momenta pi.)
The special theory of relativity did not include accelerating reference frames, forces or gravity. In considering how Newtonian gravitation might be modified to fit special relativity, he proposed the equivalence principle: that a gravitational field is equivalent to a uniformly accelerated reference frame. He also realized that the bending of light by gravity would be a consequence of the equivalence principle which could be tested by astronomical observation. Furthermore, the Lorentz transformations did not apply to this more general situation and that the gravitational field equations must be nonlinear infinitesimal transformations.8 This was so breathtaking that the Nobel Committee did not believe the theory to be correct! But Einstein by then was considered to be such a prolific genius that he was given the 1921 Nobel Prize in Physics “for his services to Theoretical Physics, and especially for his discovery of the law of the photoelectric effect”. The photoelectric effect is a quantum mechanical effect. Yet during his lifetime Einstein did not believe that quantum mechanics was a proper theory but the Nobel Committee did!
Quantum mechanics actually makes it possible to bring out the fundamental nature of conserved quantities and relate them to corresponding types of symmetry of the laws of physics. For each of the rules of symmetry in physics there is a corresponding conservation law in quantum mechanics: energy, momentum, charge, etc. Even the Schrödinger equation of quantum mechanics has a symmetry. This equation is unchanged if the phase of the wave function 
is shifted by an arbitrary constant That is, you will not be able to detect any difference between a system described by 
and another by 
In fact, this symmetry is related to the conservation of electrical charge.
These are among the most beautiful and profound things in physics.
In classical physics, energy E, momentum p, and angular momentum M appear as functions of the velocity v and coordinates r of a body of mass m as :
from which it follows that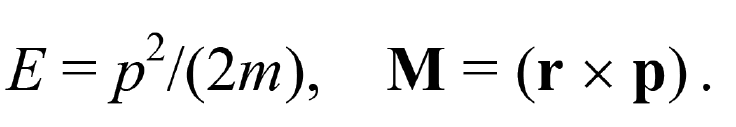
However, when we go into the microworld of quantum mechanics, the very concept of the velocity of an object becomes unsuitable and these formulas become pointless. At the same time the conserved quantities (E, p, M) retain their meaning both in classical and quantum mechanics.
However, it is important to note that in quantum mechanics (E, p, M) are, generally speaking, not expressible in terms of each other. The second expression, namely
does not hold in the microworld, since a micro-object has no states in which the values of momentum and coordinates can be specified simultaneously. This follows from Heisenberg’s uncertainty principle. The first expression, namely
is valid only for the free motion of a micro-object.
For a bound micro-object (say, an atomic electron) the energy is quantized, with the result that for each energy level we cannot indicate a definite value of momentum.
In 1928 Paul Dirac (1902-1984) wrote down an equation, which combined quantum theory with special relativity to describe the behavior of an electron. His equation had two possible solutions, one for an electron with positive energy, and another for an electron with negative energy. Rather than abandon his equation, he boldly interpreted the electron with the negative energy to imply that for every electron there must be an anti-electron, identical in every way but with a positive electric charge. To postulate the existence of matter-antimatter was an amazing belief in symmetry in the laws of Nature.
It turns out that without antiparticles, the equations of theoretical physics describing the various types of elementary particles would not be invariant under the Lorentz transformation. So the electron has an anti-electron (positron), the proton has an anti-proton, the photon is its own anti-photon, etc. The positron was later experimentally discovered by Carl David Anderson (1905- 1991) at Caltech in 1932.
Paul Dirac was awarded the 1933 Nobel Prize in physics for predicting the existence of positrons and electron spin. In his Nobel Lecture, Dirac speculated on the existence of a completely new Universe made out of antimatter! Carl Anderson was awarded the 1936 Nobel Prize in physics for his discovery of the positron.
Anderson’s PhD thesis at Caltech was on photoelectrons produced by x-rays. About Robert Millikan (Nobel Prize in Physics 1923; oil drop experiment) who supervised his thesis, he once wrote, “For this I thanked him, but not once during the three years of my graduate thesis work did he visit my laboratory or discuss the work with me.” In his post-doctoral work, again, loosely supervised by Millikan, Anderson built and ran the Caltech Magnet Cloud Chamber. Using the Cloud Chamber, in 1936, with Seth Neddermeyer, his first graduate student, Anderson also discovered the positive and negative “mesotron,” now called the muon.
CPT-symmetry is a conservation law for the combination of three sufficiently clear symmetries: the symmetry with respect to the replacement of all particles by their respective antiparticles (charge conjugation symmetry or C-invariance), mirror symmetry (space parity or P-invariance), symmetry with respect to time reversal (T-invariance). CPT-symmetry means that if all particles were simultaneously replaced by appropriate antiparticles
and mirror reversed, and then the sense of time were reversed, the laws of physics would remain unchanged and all the physical processes would proceed as before. As Abraham Pais9 has noted, if CPT-symmetry turns out to be untrue then “all hell will break loose.” 10
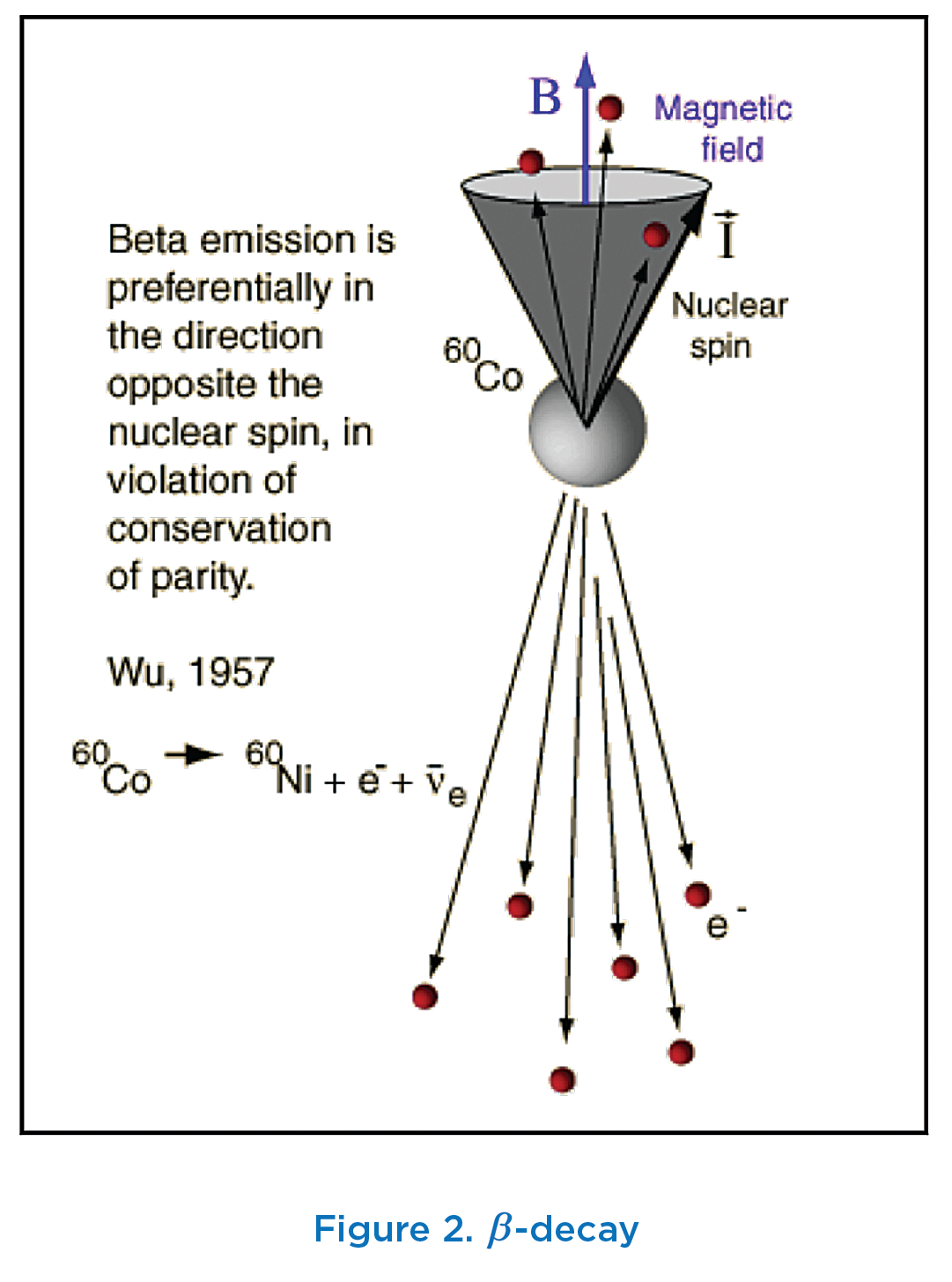
Up until 1956, it was believed that mirror symmetry was a natural invariant of nature. That is, the laws of nature were invariant with respect to mirror symmetry (space parity or P-invariance). In 1956, Tsung-Dao Lee and Chen Ning Yang, suggested that mirror symmetry cannot apply to the group of laws that describe 
the decay of elementary particles.11 This was confirmed by a direct experiment in January 1957 by Chien-Shiung Wu and her associates. This was intriguing since it meant that in some phenomena, nature exhibits left-right asymmetry.
Wu’s beta decay experiment: “By lowering the temperature of cobalt atoms to about 0.01K, Wu was able to ‘polarize’ the nuclear spins along the direction of an applied magnetic field. The directions of the emitted electrons were then measured. Equal numbers of electrons should be emitted parallel and antiparallel to the magnetic field if parity is conserved, but they found that more electrons were emitted in the direction opposite to the magnetic field and therefore opposite to the nuclear spin.”12 (See Figure 2.) Thus they found a clear mirror-asymmetric relation between the distribution of emitted electrons and the spin directions of the cobalt nuclei.
The Nobel Committee promptly awarded the 1957 Nobel Prize in Physics to Yang and Lee.
In the 1940s while he was based at the Chicago University’s Yerkes Observatory in Williams Bay, Wisconsin, S. Chandrasekhar drove more than 100 miles round-trip
each week to teach a class of just two registered students— T.D. Lee and C.N. Yang. In 1957 the whole class (Yang and Lee) won the Nobel Prize in physics “for their penetrating investigation of the so-called parity laws which has led to important discoveries regarding the elementary particles”! S. Chandrasekhar received the 1983 Nobel Prize in Physics “for his theoretical studies of the physical processes of importance to the structure and evolution of the stars”.
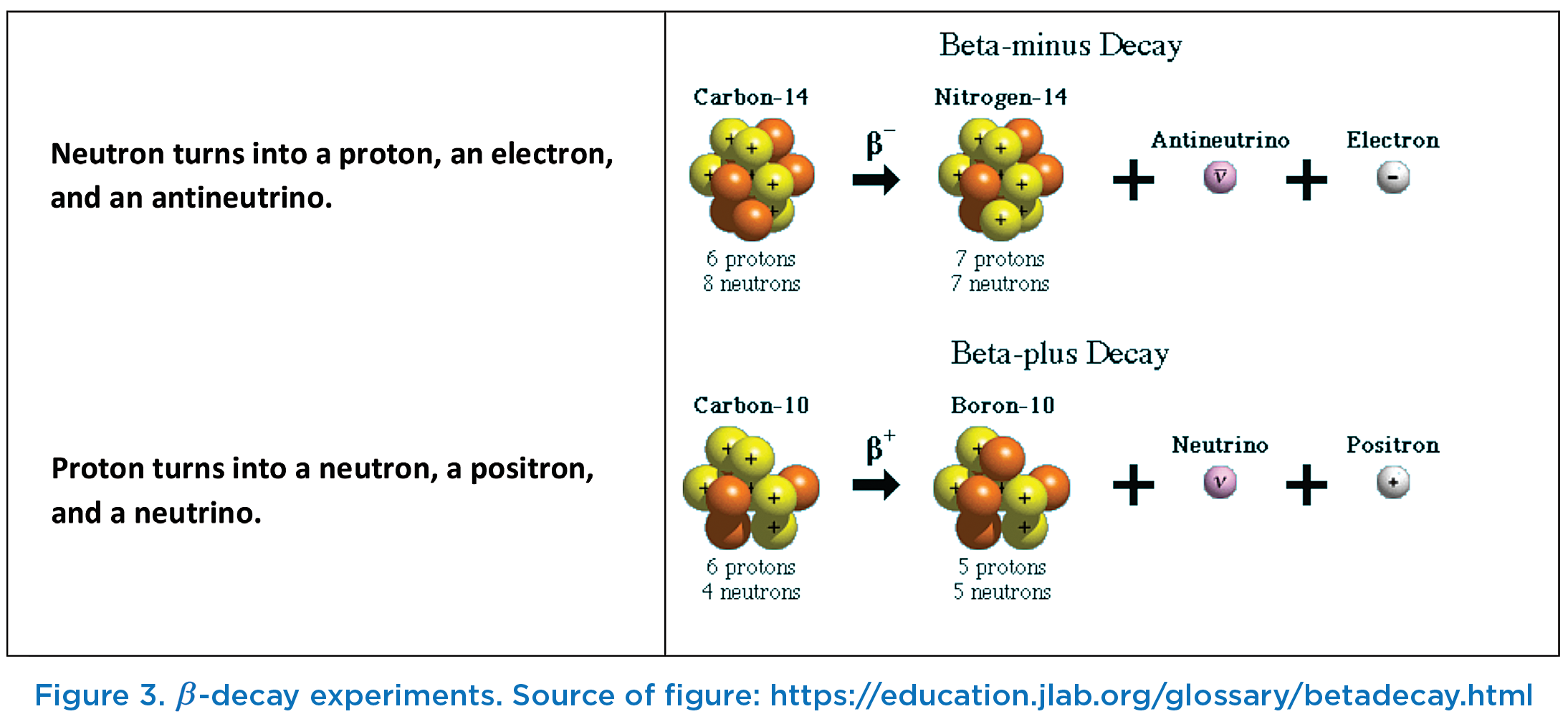
It turns out that mirror symmetry is regained if we account for the existence of anti-matter. Matter to the right is symmetrical with anti-matter to the left. This has been verified in -decay experiments, using positron decay instead of electron decay.13
Stereoisomers are compounds that have the same empirical and structural formulas but differ in the three-dimensional arrangement of the atoms. In one important form of stereoisomerism two molecules have the same structural formula but one is the mirror image of the other (enantiomers). See Figure 4.
The existence in nature of left- and right-handed molecules was suggested by observations of the rotation of polarization planes. Amino acid molecules in human cells are always left handed. The right-rotating enantiomer is labeled D-, and the left-rotating, L-.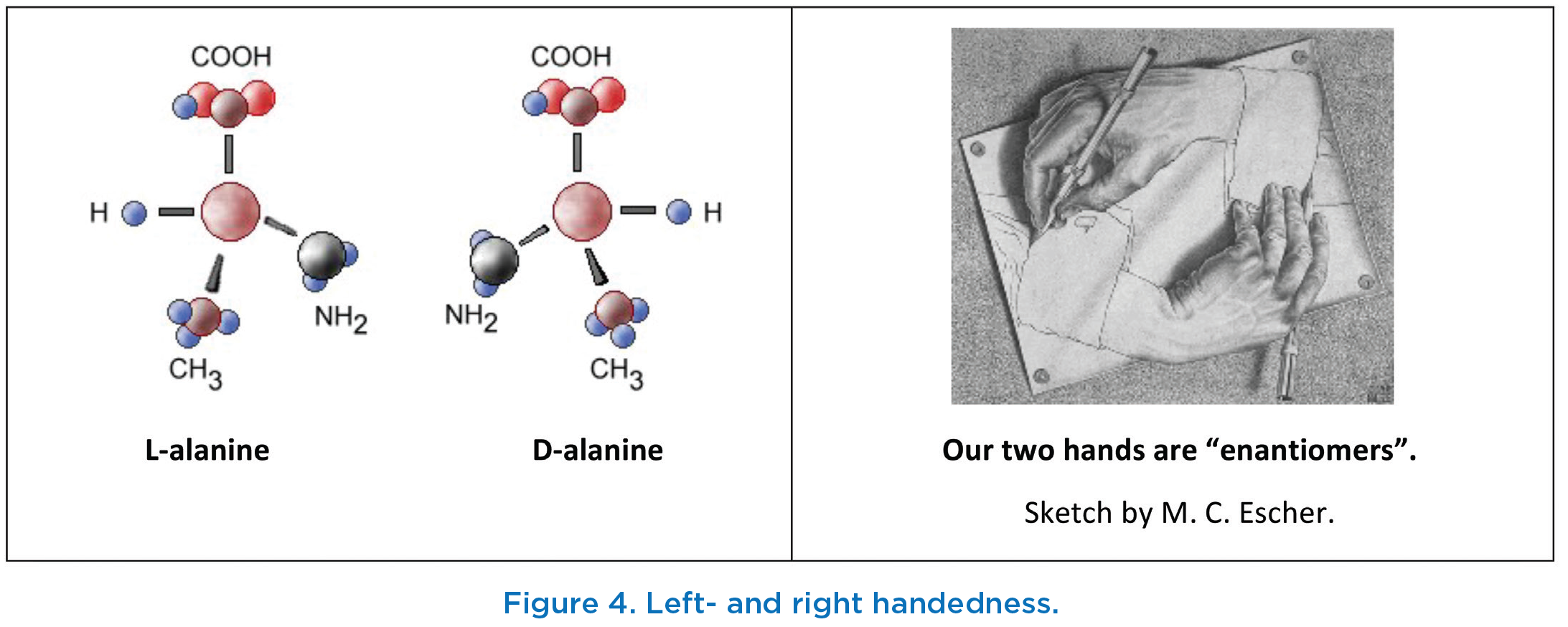
Aristotle in his book The Physics said that bodies that occupy places that are not natural for them are impelled to move, whereas those in their natural places are not. No natural motion can exist, if every point of space is equivalent. He also denied the existence of a vacuum. He reasoned that in a vacuum (i.e., in a uniform space) nobody can say why a body set in motion would stop, for why should it stop in one place and not another? He also refused to accept the notion that time is independent of events. He reasoned quite simply that time cannot exist without change. Newton considered space to be a void arena of things and phenomena. It was 3-dimensional, continuous, static, infinite, uniform, and isotropic. He believed that absolute space, in its own nature and with regard to anything external, always remains similar and unmovable. In his view, time was also absolute and independent. He regarded it to be the “receptacle of events” and that the course of events did not affect the flow of time. Time was uni-dimensional, continuous, homogeneous, and infinite.14
Historically, theorists in natural sciences, and particularly in physics, have preferred those theories, which stand out as having logical elegance and beauty. Beauty is subjective and has no rigorous value, but the first quality is objective to the extent that it can be used in practice. In addition, they prefer simplicity, which is again subjective.
Our search for knowledge is now rooted in ‘Look for simplicity, look for beauty, look for symmetry’.
In the 20th century, physicists have, one may say, been obsessed with invariances that govern nature, seeing in them both beauty of symmetry and deep simplicity. One naturally wishes to select the conserved quantities as the physical quantities with which to describe nature.
Another way of looking at the laws of nature is that they are laws of prohibition, that is, they prohibit any phenomenon that would change the conserved quantity. Today, physicists look for as many symmetries in nature as they can. It is a guiding star in their speculations. Lack of symmetry, when intuitively expected, brings a troubled look on their faces. When we identify an object, in spite of distortions, additions, and deletions, we do it on the basis of some invariant qualities of the object, that is, we identify them on the basis of symmetry.
Science is beautiful when it makes simple explanations of phenomena or connections between different observations.
— Stephen Hawking
[1] This paper is an edited version of a public lecture delivered by the author on 05 July 2019 at Bangalore. The lecture was devoted to understanding what we mean by symmetry in mathematics and the central role it plays in our perception of the universe.
[2] Noether, E., Invariant Variation Problems (M. A. Tavel’s English translation of “Invariante Variationsprobleme,” Nachr. d. König. Gesellsch. d. Wiss. zu Göttingen, Math-phys. Klasse, 235–257 (1918), which originally appeared in Transport Theory and Statistical Physics, 1 (3), 183–207 (1971)), reproduced at arXiv:physics/0503066 v1 8 March 2005. http://arxiv.org/PS_cache/physics/pdf/0503/0503066v1.pdf
[3] Garavelli, J. S., Hilbert’s Space: aspects of one century and prospects for the next, Retiring President’s Lecture, 14 January 2000, Philosophical Society of Washington.
[4] Danos, M. Ward-Takahashi identities and Noether’s theorem in quantum field theory. Foundations of Physics, July 1997, Vol. 27, No. 7, pp. 995-1009. “The gap in the mathematical derivation of Noether’s theorem, and also of the Ward-Takahashi identities, caused by performing variation before quantization is closed by introduction of variational calculus for operator fields. It is demonstrated that both Noether’s theorem and the Ward-Takahashi identities retain full validity in quantum field theory.”
[5] For a brief description of gauge invariance, visit Viktor T. Toth. The principle of gauge invariance. 19 November 2003. http:// www.vttoth.com/gauge.htm and http://en.wikipedia.org/wiki/Gauge_theory
[6] Feynman, R, Leighton, R., and Sands, M. Feynman’s Lectures on Physics, Online edition, 2013. Lecture 15, Section 15-8. https:// www.feynmanlectures.caltech.edu/
[7] Lorentz contraction is the physical phenomenon of a decrease in length detected by an observer in objects that travel at a non-zero velocity relative to that observer.
[8] Garavelli, J. S., Hilbert’s Space: aspects of one century and prospects for the next, Retiring President’s Lecture, 14 January 2000, Philosophical Society of Washington. https://pswscience.org/meeting/hilberts-space-aspects-of-one-century-and-prospects-for-the-next/
[9] Abraham (Bram) Pais (May 19, 1918 – July 28, 2000) was a Dutch-born American physicist and science historian. He coined the term ‘baryon’ to denote a type of strongly interacting particle that includes the proton and neutron in the atomic nucleus.
[10] Tarasov, L. This Amazingly Symmetrical World. Mir Publishers, Moscow, 2018. https://ia800704.us.archive.org/12/items/TarasovThisAmazinglySymmetricalWorld/Tarasov-This-Amazingly-Symmetrical-World-Mirtitles-2018.pdf
[11] A free neutron decays into a proton, an electron, and an antineutrino in an average of about 15 minutes. The process is known as -decay. For historical reasons, the electron is referred to as the -particle. This is an example of weak interactions mediated by the photon analogues W and Z bosons. Weak interactions are also responsible for the radioactive decay of a uranium U238 nucleus which disintegrates spontaneously into a thorium and a helium nucleus ( particle) on an average of 5 x 109 years.
[12] Source of figure and quote: http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/parity.html#c2
[13] Feynman, R., Leighton, R., and Sands, M. Feynman’s Lectures on Physics, Online edition, 2013, Vol. 1, Chapter 52, Section 52-8. https://www.feynmanlectures.caltech.edu/
[14] See, e.g., Vladimirov, Yu., Mitskievich, N., and Horsky, J. Space, Time, Gravitation. Mir Publishers, 1987 (English translation), p. 13.
