Prashanth Hebbar, Managing Partner, Knobly Consulting

---

POSIT is knocking on the doors of IEEE 754 standard for Floating Point Arithmetic promising “honest”, accurate answers as compared to compromised, “precisely inaccurate” answers provided by the latter. A battle is brewing among numeral analysts and semiconductor engineers on whether to embrace this bold new approach or not. This is a quick look at POSIT based on an interview with its inventor of POSIT, Prof. John Gustafson, A*STAR Computational Resources Centre and National University of Singapore (joint appointment), Singapore.

If Prof. John Gustafson has his way, you may be talking about Tera POPs instead of Tera FLOPS with respect to your “High Performance Computing” prowess to crunch very large float numbers. The buzz is now out that Prof. Gustafson’s POSIT data type is a serious contender to usurp the nice perch enjoyed by IEEE 754 specification for floating point arithmetic which is the industry standard.

“POSIT, stands for, as per the Oxford American Dictionary, a statement that is made on the assumption that it will prove to be true,” says Prof. Gustafson, who is travelling the world meeting academics and researchers and coopting them into his new scheme for floating number arithmetic. ACCS hosted Prof. Gustafson’s distinguished lectures in India at the Indian Institute of Science, PES University and IIT Madras in November 2017.
“This idea has been knocking around inside my head for the past 30 years. I have put in my complete energy to take this forward the last seven years,” says Prof Gustafson. Ever since he saw the William Kahan’s scheme to handle floating point arithmetic by computers which later became the IEEE 754 Standard, Prof. Gustafson then a researcher in IBM, has thought that there should be a better way to do float arithmetic. I always thought, “It just did not sound natural and logical. Why should we go through such roundabout way to achieve half precision and end up in best guess result.”
“Can we start calling it ‘posits’,” quips Prof. Gustafson when I call a number a float. In a way highlighting the amount of re-education he has to do to get his idea fly. “Until I wrote a book called ‘End of Error’,” people didn’t take POSITs seriously. When the book with that title appeared people were curious to know who can be so preposterous as to predict end of error; it was like predicting end of the world,” recalls Prof Gustafson. While the End of Error became a bestseller, a rare fare for a mathematical book, and it also drove Prof Gustafson’s biggest critique William Kahan to finally react. Kahan’s lengthy rebuttal, which is a google away, finally brought focus to the claim of POSIT.
“Did you ever get to talk to Kahan in person about this,” I ask Prof. Gustafson and he points me to a debate which is recorded and available on Youtube. “He is a tough person to talk to,” says Prof Gustafson.
So what exactly is Prof. Gustafson talking about and why is Kahan angry. To get behind the story we have to go into some of the idiosyncracies of the Floating Point (IEEE 754) and compare it with what Prof Gustafson proposes with his repertoire of Unums I, II and III and Posit. So fasten your seatbelts for a quick roundup of these concepts.

The shortcomings of IEEE 754

Call it a compromise to get things moving or not but IEEE 754, which has become the industry default for floating point arithmetic with all the chip makers adhering to its scheme, has some annoying behaviours. Much of it these annoyances aren’t appreciated unless we are working with higher precision numbers. The most cited being the rounding error. Rounding error has played havoc since Floating Point is dependent on the user machine’s precision. So it attempts to fit every given number into the allowed number of bits by rounding the number using any of the four principles – rounding up to the nearest next number, rounding down to nearest previous number or rounding to zero. Some times, it simply drops the last bit without warning to fit the number to the machine’s precision.

Examples of numeric Errors:

Consider a number, 44.85 x 106 is represented as a normalized floating point as .4485 x 108 Pictorially, one can imagine the number to be represented as below. 

Example 1 showing rounding errors

Let us assume a given computer can handle a mantissa of up to 4 digits and an exponent part up to 2 digits. Any arithmetic operations that increases the mantissa to more than 4 digits will end up in a rounding up or down condition and if this rounding is far from our expected value, it obviously results in an error, called a rounding
error.
Similarly, any operation that increases the number of digits to represent the exponent part beyond 2 will result in an overflow (if the sign bit is positive) or underflow (if the sign bit is negative) error.
The second is the overflow and underflow where the exponent values do not fit the bits allocated for it and it raises an unexpected error.
The IEEE 754 standard’s biggest drawback is that it sometimes does not obey arithmetic laws of associativity and commutativity. So, a proven algorithm with different addition and multiplication priorities may show different results on different machines.
Non-conformance of Law of Associativity & Distributivity

Since rounding up or rounding down is the essential part of the Floating Point operations, associative and distributive laws do not hold good. Hence,
(a + b) ± c (a – c ) + b
a(b – c) (ab – ac)

Example 2 showing non associativity

One can safely say that the floating point arithmetic has brought about an interesting sub field where one studies the Errors in Numbers. Due to the way it is defined, perhaps good for its time, the results we get from Floating Point arithmetic is not accurate but an approximation. Of course, depending upon the precision of the user’s machine, we can set this approximation closest to real value.

Not so much for researchers and high precision engineers where every digit far away from the decimal point matters.You can, in fact, read an interesting case of how a double precision IEEE 754 standard treats the operation 0.1 + 0.2 giving an answer of 0.30000000000000004 while one would expect a simple 0.3. See below a discussion in contrast to how Type I Unum handles this.

Number theorists have come up with a set of interesting handy thumb-rules to handle errors
arising from floating point numbers.
1. x + x … n times is usually less accurate than nx
2. Avoid taking differences of two nearly equal numbers whenever possible
3. Avoid formulating an algorithm that tests whether a floating point number is zero
4. Always check for numerical instability whenobtaining a numerical algorithm
5. Use double precision when you cannot loss
Prof. Gustafson embarks to overcome this challenge and come up with a system which promises better precision and accuracy; an approach that is supposed to take less bits than IEEE 754 and thus less energy in nanojoules.
In his first attempt, he offered a drop-in replacement to IEEE 754 called the Unum Type I. “All I am saying is Unum Type I can be seen as a simple extension to IEEE 754,” says Prof Gustafson. “I am not even talking about [Unum] Type II and III for that matter.” Unum Type I keeps the IEEE 754 scheme and comes up with three additional tags called the Utags (Unum Tags). While an IEEE 754 Float has a single bit to denote a sign, exponent bits and mantissa bits, Unun Type I has ubit, exponent size bits fraction size bits in addition to what the IEEE 754 Float Point number prescribes.

Ubit is a flag that tells us whether there is more decimals coming along or not – 0 for no more decimals and 1 means more decimals to come. The fraction-size and the exponent-size provides a variable width storage for both fraction and exponent. Thus ensuring the unums cover the whole range from -Infinity to +Infinity.
So, how exactly is Type I Unums different from IEEE 754 apart from adding utags. “It’s a whole lot different than the Floats,” says Prof Gustafson. “If you ever wanted an exact answer to an Floating Point arithmetic operation you would never get it simply because on different machine they may vary differently.” “Whereas in Unum arithmetic, either you have an exact number or an interval within which that number falls but not an approximation.”

So, if you whip up a Julia terminal and run the following command:
x = unum22(1.0)
you get
1.0
As the answer.
If you do
y = unum22(2.1)
Surprise, surprise, you get
(2.0,2.125)

This is not the answer one would expect. With Unums where there is uncertainty, we get an interval. Now, you may ask, what uncertainty could be there in representing the decimal number 2.1. Well, in Float64 precision or Float32 bit precision, 2.1 cannot be expressed “exactly”. Here “exactly” means just what it means. Both Float 64 bit and Float 32 comes close to 2.1 but not exactly. Unum, on the other hand understands this since its ubit is set to 1 which means the value is not exact and hence gives an interval. If the programmer prefers better precision he simply increases the exponent and frac sizes and comes ever closer to the answer.
This can be illustrated better with another operation. In your Julia terminal and the Unums package installed, do the following:
a = 1/3
Now, since you are already primed to the exact and uncertain situations, you will expect an interval and there it is

Unum22(1/3) gives you
((0.328125, 0.34375)
Whereas, your Float operation
1/3 gives you
0.3333333333333333

And other Unum operations gives you the following results
x + y (3.0,3.125)
x/y (0.46875, 0.5))

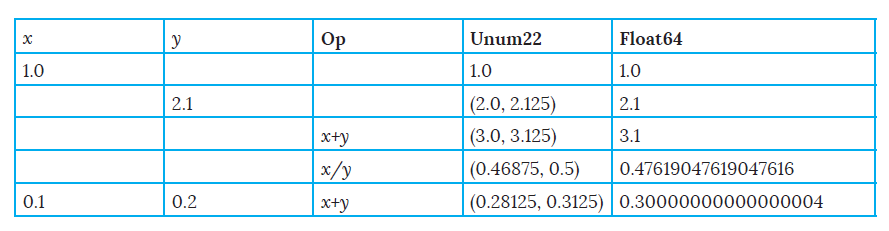
The table above contrasts the two operations quite vividly and demonstrates Prof Gustafson’s assertion: “a precise answer is not an accurate answer.” Float arithmetic attempts to give a precise answer fitting its value to the underlying machine’s precision. Whereas, Unum arithmetic attempts to give an accurate answer irrespective of the underlying machine’s precision. In fact, it falls back on an age-old approach of interval arithmetic to compute its results. “The Unum answer is more honest because the actual answer is contained in the interval,” says Prof. Gustafson.
There are, however, issues with Interval Arithmetic which Prof Gustafson says can be overcome with the concept of ULP (Unit to the Last Place). Since it is out of the scope of this essay, we will not go into it. Readers are welcome to investigate it independently (see bibliography).
Meanwhile, Prof Gustafson has introduced Type II Unums and Type III Unums and the concept of Valids and finally Posit which improve one upon the other gradually. For example, Type II Unums break away from IEEE 754 standard and uses a new notation to build the the number system with the aid of SORNs (Set Of Real Numbers) and states of a given value: Present in the set or absent in the set, exact or inexact, positive or negative. With these, a more accurate and faster results are expected. It also promises to do away with NaN (Not a Number) notation which is a major hurdle with IEEE 754). The notation to represent all the possible values using SORN is ingenius. It requires only a 4 x 4 matrix to compute all possible values from -Infy to + infy.
Aren’t floats too deeply ingrained in people’s psyche? “No, it is slowly unravelling for sure,” says Prof Gustafson. It is true that people have been quite sceptical in the beginning and as the Professor goes around talking to various groups, improving his theory, they have come round to appreciate the underlying mechanisms. But there is a second hurdle. “I need to find people who are working at the chipset level,” says Prof Gustafson. Most of the people interested in Unum and Posit are software people. Some have written libraries for various versions. Atleast one library exists in Python and 3 to 4 in Julia as of this writing. There is an attempt at a c and C++ library which does not seem to be progressing.
“We had a brilliant young engineer who had done some exciting work in Unum and Posit but unfortunately he left to join the Federal Fire Service and we haven’t been able to trace him,” says Prof Gustafson, perhaps highlighting how difficult it is to find people to work on basic numerical analysis work.
“We have already taped out a processor with reference implementation,” says Prof Gustafson but he is visibly agitated by the slowness in the industry. With so much invested in IEEE 754 standard, will the industry listen to him? “I have big hopes with ML and AI coming along,” he says. “And these things take a long time.”
Notes:

• Interval Arithmetic: In the context of Floating Point arithmetic, intervals help define a set of real numbers as possible values. Interval Arithmetic requires the set of reals be bounded on both sides. The fundamental characteristic of interval arithmetic is it favours accuracy over precision. For instance, rounding errors often seen in floating point arithmetic are
  accumulated as the interval width. This may result in loss of precision but the result is more accurate when compared to floating point.
  
  
• NaN: NaN (Not a number) is a IEEE 754 standard special value given to any values resulting from operations involving “infinity”. So ∞ – ∞, -∞ + ∞, 0 x ∞, etc. result in a NaN. Unum Type II proposal claims to do away with this concept of NaN by representing values as a set of reals.

 

REFERENCES

Gustafson, John L. “Posit Arithmetic.” 10 Oct. 2017, posithub.org/ docs/Posits4.pdf.
Rajaraman, V. Computer Oriented Numerical Methods. 3rd ed.,Prentice-Hall, 2008.
Byrne, Simon. “Implementing Unums in Julia.” Implementing Unums in Julia – Julia Computing, 29 Mar. 2016, juliacomputing.
com/blog/2016/03/29/unums.html.
Gustafson, John L. “A Radical Approach to Computation with Real Numbers.” www.johngustafson.net / presentations / Multicore
2016-JLG.pdf.
“Floating Point Arithmetic: Issues and Limitations.” Floating Point Arithmetic: Issues and Limitations — Python 2.7.14 Documentation,Python Software Foundation, docs.python.org/2/tutorial/ floatingpoint.html.
Tichy, Walter. “End of (Numeric) Error, An interview with John L. Gustafson.” Ubiquity – an Acm Publication, Apr. 2016, ubiquity. acm.org/article.cfm?id.
Gustafson, John L, and Isaac Yonemoto. “Beating Floating Point at Its Own Game: Posit Arithmetic.” Supercomputing Frontiers and Innovations, vol. 4, no. 2, 2017, doi:10.14529/jsfi170206.