Abstract

In the last few years the phenomenon of cryptocurrencies has captured the imagination of people in two dominant sectors, information technology and financial technology. These two sectors have been brought much closer due to the recent developments in both sectors. We provide an analytic view of various interconnected issues, drawing upon tenets from cryptography, digital cash, cryptocurrencies, blockchains and socio-economics of money. We discuss the underlying scientific and technical principles behind the extant methodologies, in particular the artefact Bitcoin.

The socio-economics and governance aspects of the genre of cryptocurrencies, including the seminal earlier notions of digital cash, led us to the development of our version of electronic money termed VMcoins and its embedding it in a blockchain like system termed VSKchains. We provide a brief description of this scheme. We discuss the mathematical underpinnings of hash functions, which are the main work-horses of cryptocurrencies and blockchains. Also the digital signature primitive plays an important role in the management of blockchains. In the Appendix, we explain briefly, the basic principles of elliptic curves, an interesting object of mathematics and computer science, which plays a critical role in all functionalities of contemporary cryptographic applications.

1. Introduction

 The properties of physical money, such as anonymity, privacy, transferability, fungibility, ease and control of use, have made them a way of life for human beings. Rapid technological developments in the context of slowly changing sociological milieux, have prompted human ingenuity to come up with novel solutions to the handling of money matters.

The initial technical developments in the field of cryptography, namely ecash, provide many new ways of handling digital money analogous to the ways of using physical money. These employ the principle of cryptographically secure pseudo-random sequences called hash chains. The seminal results of David Chaum, in 1982, led to a spurt of exciting ideas and potential applications of digital cash during the subsequent two decades. However, all these ideas needed to wait, for blooming, for the coming of the mobile communication and computing platforms. Meanwhile the fiscal instruments of digital commerce and trading (or widely known as e-commerce and m-commerce) had found the convenient solutions of plastic card based transactions.

The digital cash phenomenon made a forceful reappearance in a different form Bitcoin, and its ilk, during the last 7 years. These forms of digital currency, termed cryptocurrencies, which are members of the broader family of digital entities termed blockchains, are current technological torch-bearers. In this article, we trace the technical developments in these two tracks of ideas. We also point to our our works (i) on transferable digital cash, and (ii) on a version of cryptocurrency that seeks to strike a balance between completely, decentralized (or distributed) private fiscal instruments and state-mediated fiduciary instruments.

In both forms of digital cash, the technical aspects get intertwined with other sociological features. Such a situation is prevalent, in any sector, when an innovative, new technology  The properties of physical money, such as anonymity, privacy, transferability, fungibility, ease and control of use, have made them a way of life for human beings makes appearance. We discuss the salient issues with a view to highlighting the pros and cons and hence forecasting the future of the exciting topic of cryptocurrencies.

In Section 2, we trace the evolution of digital cash, a cryptographic token, analogous to a coin, or a coupon, which can be used as an instrument of exchange for digital payments. Such a digital form of money was a precursor to the contemporary phenomenon of cryptocurrency. We devote Section 3, to a description of a canonical example of this genre of money, the Bitcoin. We also note the wave of alternative cryptocurrencies. In Section 4, we first discuss certain aspects of monetary transactions with physical fiat cash instrument issued by the state. This paves the way for discussions on digital currencies, fiat or private. Then we describe our proposal for a variant of the private currency genre, which could serve as a template for state regulated cryptocurrency, as well. In the closing Section 5, we make a summary examination of the future of blockchains and cryptocurrencies. Finally, in the Appendix, we explain briefly, the basic principles of elliptic curves, an interesting object of mathematics and computer science, which plays a dominant role in contemporary cryptography. Elliptic curves are being used routinely, to provide information security functionalities, in many software products such as SSL, WhatsApp, Bitcoin, Ethereum and other cryptocurrencies.

2. Digital Cash

 Money plays a central role in the conduct of human affairs. Money in the form of cash, as a store-of-value and as a medium of exchange, also referred to as currency, takes many forms. These forms have evolved over centuries among civilizations, from physical tokens to state issued denominational, fiat currencies of universal acceptance. The physical instruments co-exist with other non-physical forms of instruments, based on denotational, legal, political, economic and governance principles. The advent of computer, communication technologies in human activities of trade and commerce, brought new perspectives on money matters. The transactions using the physical cash instrument has many useful features such as privacy, anonymity, peer-to-peer, fungibility and ease of use. A notable input from the scientific community was digital or electronic cash (ecash).

Many electronic payment systems using the payment instrument of ecash, were proposed soon after the seminal work of D.Chaum, in 1982, on ecash. They are classified into two types, viz, online and offine. Online e-payment systems are those in which the transfer of electronic money between the payer and payee takes place in the presence of a third party, usually a bank, that guarantees the authenticity of the coins being transferred. In contrast, in offine systems the transaction occurs between the two parties, payer and payee, alone. The money transferred is verified when the payee deposits the coins with a bank.

We briefly review some of the ecash based payment systems. For brevity, we choose only the major systems [10] , [11] Certain other related and interesting systems are [2],[21],[23],[25],[8] David Chaum’s ecash[11] is a fully anonymous, secure online electronic cash system. It implements anonymity using blind signature techniques. The ecash system consists of three main entities:

•   Banks who issue coins, validate existing coins and exchange real money for ecash.
•   Buyers who have accounts with a bank, from which they can withdraw and deposit ecash coins.
•   Merchants who can accept ecash coins in payment for information, or hard goods. Merchants can also run a pay-out service where they can pay a client ecash coins.

 
To withdraw a coin, the user generates a coin(message), m, consisting of a random serial number, r, multiplied by a blinding factor, b, and the denomination. This message, m, is signed by user using his private key and sent to the bank after encrypting the message using the bank’s public key. The bank signs the blinded coin and debits the user’s account. The user un-blinds the coin by dividing by an appropriate blinding factor. Thus the bank cannot link the ecash to the user. While spending, the coins are securely transferred to the merchant. The merchant verifies the coins by sending them to the bank.  To withdraw a coin, the user generates a coin (message), m, consisting of random serial number, r, multiplied by a blinding factor,b, and denomination. This message, m, is signed by user using his private key and sent to the bank after encrypting the message using the bank's public key After ascertaining that the coins are not double spent, the bank credits the merchant’s account and the coin is destroyed. If the coin is double spent the bank sends an appropriate message to abort the transaction. The advantage of ecash is that it is fully anonymous and secure as it uses public key cryptography. The downside is that the database of spent coins gets bigger and new coins have to be issued for every transaction.

Stefan Brands proposed an offline ecash payment system [8]. In this scheme, three participants are involved : the computer at the bank, computer of an Internet service provider and the machine of the user. The user’s machine is interfaced with a tamper resistant device. The tamper resistant device increases the counter at withdrawal time by the amount that is withdrawn and decreases the counter when a payment is made. To make a payment from the user to the Internet service provider and for the latter to verify that the payment is genuine, a secret key is installed in the device. When a specified amount is transferred this key is used to sign the amount. The service provider can now use the bank’s public key to verify the authenticity of the electronic money so transferred. The user does not know the secret key and hence cannot produce the signature. After the digital signature is verified, the service provider accepts and provides the requested service to the user. The advantage of this system is that no transaction requires the presence of a third party for the verification. Thus offline operation provides lesser communication overheads. But if the device is broken by anybody then it would necessitate a change of device for every user of the system.

Transferability of coins is a difficult feature in most of the ecash systems, whether online or offline. This is due to the fact that double-spending by copying digital cash instruments is trivial as opposed to situation with physical cash. In ecash payment systems usually the lifetime of a coin is the lifetime of the transaction it is involved in. This is in contrast to physical cash where the money retains its value over several transactions and merely changes ownership. An obvious advantage of transferable cash is that a coin issuing authority need not issue new coins for every transaction that takes place.

A concern in the early years was the enormous load that would be placed on the central bank or coin-issuing authority that would check the authenticity of coins. This as certainly a bottleneck since each coin in a transaction needed to be verified by a central server. We proposed a scheme [26] in which we replaced a central verifying server with a set of trusted servers, thereby distributing the load across several entities. We also required a dispute resolving mechanism in place for the electronic payment system. Given the fact that the payer and payee do not know each others’ real identities as they transact over the Internet, the payment system should be able to give guarantees to both the parties in the transaction. We outlined such a dispute resolution protocol as a part of this payment system.

In the next section we describe a current, modern version of digital currency called the Bitcoin. The Bitcoin invention takes advantage of the cryptographic principles of ecash design and combines these with distributed database operations.

3. Cryptocurrencies

 The inventors of cryptocurrency have also taken the path of generating (or minting) the fiscal instrument of digital currency. Thus they take on the role of a central bank. We trace the developments in this world of cryptocurrencies. The Bitcoin, which is the first such cryptocurrency, has received much attention from the computer technology and financial technology aspects. The recent publication [3]. covers the theory, design and applications of the Bitcoin in detail.

3.1 Evolution of Modern Cryptocurrency

The Bitcoin is the first completely decentralized anonymous cryptocurrency. This also solves the problem of double-spending in digital cash. The Bitcoin was proposed by Satoshi Nakamoto in 2008 [22]. The Bitcoin network came to life in 2009 and people slowly started adapting to it. It is a decentralized, anonymous, publicly auditable, digital monetary, peer-to-peer payment system.

The clearing (or processing) of payment transactions involves construction of consensus blocks using a process called mining. A mining node in the Bitcoin network, that creates a new consensus block is awarded with new bitcoins (BTC). Hence this process is called minting coins. The number of BTC awarded to a mining node for creating a new block will be halved every 210; 000 blocks (approximately every 4 years). Each block is linked to the previous block by containing the hash value of the previous block, hence forming a chain of blocks called a blockchain. Hence the blocks which are sufficiently below in Bitcoin blockchain are irreversible. Hence integrity of all processed transactions are achieved.

In 2009, the Bitcoin network started with rewarding 50 BTC for each new block. As on September 2017, each new block creation led to minting of 12:5 BTC. The length of Bitcoin blockchain is reaching 0.5 million and the total size is around 150GB (including the index tables). The number of bitcoins in the system is capped at a value of 21 million and this is expected to be reached by 2140.

3.2 Bitcoin

 In this section we give a general description of Bitcoin system. The Bitcoin network is a decentralized trust network allowing peer-to-peer transactions of bitcoins between wallets. The overview of Bitcoin network is given in the Figure 1.

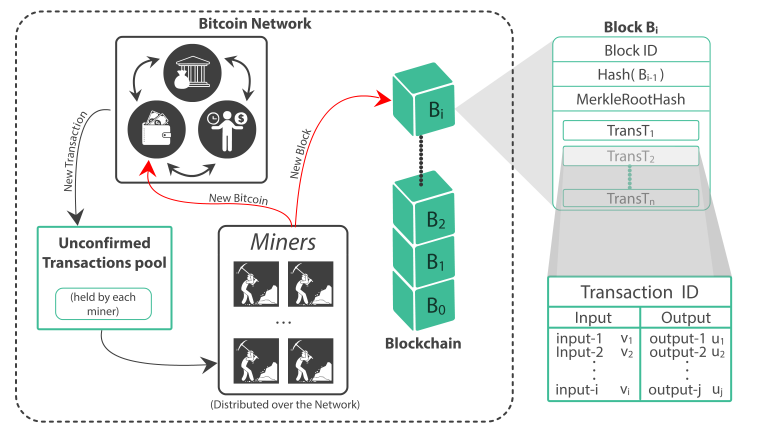
Figure 1: Bitcoin Network

 
Following is a brief description of the working of the Bitcoin system.
 
1. Each user in the Bitcoin network owns a wallet. This wallet contains several bitcoin addresses. Each address is derived from a public-key private-key pair (see Appendix A) of the user, which is used to claim ownership and authorize the transfer of a bitcoin.

2. When a user U does a transaction in Bitcoin, the wallet generates a new transaction T. An input entry in the new transaction refers to the transaction ID of some unused bitcoin owned by U. The output entry consists of the new owner’s address and the value of BTC being transferred.
 
User U will broadcast T to his neighbours. Each neighbour will check the correctness of T and forward it to their neighbours.

3. Each miner in the Bitcoin network holds a pool of unconfirmed transactions. When a miner receives T, it will insert T into the unconfirmed transactions pool held by it.

4. Each miner will try to extend the Bitcoin blockchain by constructing a new block, say B_i. The header of Bi will contain the hash of the header of last block B_i-1 in the Bitcoin blockchain, hence forming a kind of a chain.
 
The new block B_i is constructed by a procedure called proof-of-work (Section 3.3). As more and more blocks are added to the Bitcoin blockchain after B_i, it will be exponentially difficult to make changes to B_i.

5. Each miner tries independently to extend the Bitcoin blockchain by constructing a new valid block. Hence the Bitcoin blockchain may grow independently and differently at different parts of the network. As these new blocks flood the whole network, the longest chain will be accepted in due time.

3.2.1 Some additional features

 1. A bitcoin has no physical/digital identity as such. It is always referred to by a transaction ID in which it got created as the output bitcoin value.

2. The first block in the Bitcoin blockchain is called genesis block. This is a fixed block.

3. Addition of each new block following the block B containing the transaction T leads to additional confirmations. It is computationally difficult to reverse or make changes to a transaction T if it has 6 or more confirmations, i.e., there 6 more new blocks following the block containing T. Since on an average 10 minutes are required to create a new block, it takes an hour to come to conclusion that the transaction T can not be reversed or modiifed.

4. The current estimated number of hashes per second is about 8 * 10¹⁸ by the whole network (https://blockchain.info/charts/hash-rate) (In comparison, the fastest supercomputer in India, situated in the campus of IISc[27].delivers a peak throughput of 1 peta flop per second, i.e., 10¹⁵ floating point operations per second).

5. The algorithm for proof-of-work involves repeatedly hashing the header of the block and a random number using the SHA256 cryptographic algorithm until a solution matching a predetermined pattern emerges. e.g., the hashes of two successive blocks Hash are
0000000000000000003cfce1589a2d562454053bcb5214ce30c33ccd1373e7 0000000000000000007c967588995c736bcacd1e44c487f916ac3945c152132e

6. Notice that the two hashes have the same leading 72 = 18 × 4 bits of zeros which implies that getting the second hash value from the first hash value is expected to take 2⁷² computations.

7. An accounting exercise to tally the speed mentioned above, which is 10 * 60 * 2^62.8 â‰ƒ 2^72.02, shows that this huge order of computational effort required to obtain desired proof-of-work.

3.2.2 Transactions

 Every new transaction T contains entries similar to those in a double-entry bookkeeping ledger system. It contains several input and output entries. Each transaction structure is T = < I₁, I₂, …, I_j , O₁,O₂, …,O_k,>, where I_i and O_l represent input and output bitcoin values, respectively. Each I_i refers to a previous unspent bitcoin transaction ID owned by the sender (along with witness for ownership). Each O_l contains the receiver’s address (in the form of a script which can be verified by receiver’s public-private key pair) and the value of bitcoin to be transferred. At this point the contents of the transactions are hashed, to serve as an integrity check, and also as an unique identifier for the transaction. This hash value is used to generate signature (Appendix A) using the private key of the sender. The signature serves the purpose of establishing ownership.

The smallest value of BTC allowed in a transaction is one satoshi, and it is equal to 10^-8 BTC. The difference in the sum of input BTC values and the sum of output BTC values will be the transaction fee. This transaction fee will be credited to the address of the miner who successfully creates a block containing the transaction T.

Similar to the process of making change of bigger denomination notes, we can create BTC changes. The simple structure of input and output entries allows making change (or splitting) of a bitcoin. This is done by including an output entry containing the current owner bitcoin address and the remaining change value.

3.2.3 Merkle Hash Tree

 For an efficient search of a transaction in a block, the Merkle Hash tree data structure is used. It is constructed using the hash value of transactions of a block as the leaf node of a binary tree. An internal node at level j contains the hash value of ordered concatenation of the two child nodes at level j +1. Thus the root node contains the hash value of an iterated chain of hash values of the transactions in the block. The Merkle Tree structure is illustrated in the Figure 3.2.3 for a block with 8 transactions.

 

 

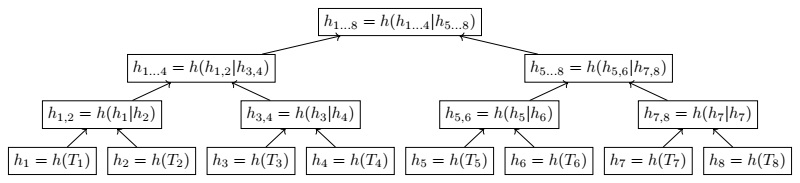
Figure 2: Merkle Hash Tree of Transactions

 
If the number of transactions in a block is n then we can query existence (and thus checking integrity) of any transaction in log₂n steps. e.g., to check the existence of transaction T₃, we need h₄, h_1,2, h_5…6, and h_1…8 hash values. The root hash value (e.g. h_1…8) in the Merkle hash tree will be included in the block header.

3.3 Consensus in Bitcoin

 Consensus in bitcoin network depends on the proof-of-work concept. This concept was first proposed by Dwork and Naor [15]. in 1992, and later (independently) by A. Back [4]. to solve email spam and denial-of-service problems. Consensus in the Bitcoin network is achieved using the principle of proof-of- work. This is discussed in the Section 4.6.

3.4 Alternative Cryptocurrencies

 With the advent of Bitcoin there is a surge in digital cryptocurrencies in the market. The website http://coincap.io/ lists more than 400 of them. Few of them, like BTC Unlimited, BTC Cash, are forked out of the original Bitcoin (now called BTC Classic). Some of the other well known cryptocurrencies are Litecoin, Zcash, Ethereum, Primecoin, etc. Many of these follow different strategies like proof-of-stake, proof-of-space, proof-of-activity, proof- of-capacity, proof-of-storage, proof-of-burn etc., for consensus.

One of the major issues with Bitcoin is that of scalability. To prevent a denial-of-service attack, the size of a block is restricted to 1MB. The time required for proof-of-work and the restricted block size both lead to a large backlog of unconfirmed transactions.

Both research community [13] , [31].. and industry community (Segregated Witness) are trying to address this issue. Anonymity in Bitcoin network is achieved by using a bitcoin address, which is computed from a randomly generated public-private key pair. The bitcoin address does not directly reveal the user identity. However this provides only pseudo-anonymity as an analysis of all the transactions may reveal some indirect information about an user identity. Some recent developments, like Zerocash [5]. and Zcash [32]., address the issues of privacy and anonymity by using non-interactive zero-knowledge proofs.

In the above discussions we have high-lighted the technical aspects of the bitcoin system covering the cryptographic security aspects of transactions and the computer science aspects of distributed ledger maintenance. There are many additional properties offered by cryptocurrencies which are not in the purview of science and technology. These properties have to do with the financial aspects (price fluctuations), the regulatory aspects (monetary exchanges, interests, taxation), legal aspects (territorial boundaries) and law enforcement aspects (contraband goods and services, money laundering). Objective research investigations are needed with respect these aspects to recognize the full power and usefulness of these cryptocurrencies.

4. Future of Money – digital and non-digital

 The gripping book, The Ascent of Money, by Niall Ferguson (Penguin, 2009), begins with a memorable sentence, “bread, cash, dosh, dough, loot, lucre, moolah, readies, the wherewithal: call it what you like, money matters.” We are interested in these matters from a technical and technological viewpoint. Actions pertaining to money engage the attention of citizenry, governments and the trading systems. Different monies, the fiduciary systems, the fisca and economic principles, the socio-political-legal issues and the psychological and technological factors are intertwined in every aspect of the human condition. Money has a long history. It ranks equally with the inventions of fire, wheel or clothing. From the first wave of barter of volatile valued artefacts man graduated to store-of-value systems based on beads, metal coins and paper notes. With the institutionalization of financial regulatory systems of treasuries of kingdoms to banking systems of governments, came the intermediate, representational forms of money in the form paper advices (cheques), plastic cards, bonds, stocks and securities. A natural consequence of the present knowledge-age is the evolution of these physical forms to digital forms sometimes known as virtual money.

4.1 Many Monies

 The closing sentence of the book by Ferguson, “… financial markets are like the mirror of mankind, revealing every hour of every working day the way we value ourselves and the resources of the world around us”, is a telling comment on the nature of our economic futures! The linguistic and cultural history of the origin and evolution of the many different monies used by different societies and peoples is as rich as the monetary values of these. There has been a close correlation between the cataclysmic events of world wars and the value of monies. The doomsday advocate, James Rickards, in his book The Death of Money, (Portfolio Penguin, 2014), builds a thesis that each financial crisis or collapse is accompanied by a period of war or unrest.

Amidst such social and financial upheavals, there have also been the positive signals of human innovation and ingenuity leading to what Schumpeter termed creative destruction. Such signals have helped societies to restore social and fiscal equilibrium. In the fiscal domain, these signals comprise different forms of monetary standards arrived at by nations. Post the second world war, the Bretton Woods convention set one such standard in the form of the US dollar. The Euro of the European Union is another recent standard. Currencies and parities of countries are set by the financial regulatory bodies of their central banks. Such state stipulated currencies are termed at currencies. The Latin word “fiat” means “so-be-it!”. Governments of countries also permit the co-existence of alternative or private currencies.

The technological enablers of a digital economy such as mobile phones and similar low-cost devices such as tablet comuters and print-of-sale (POS) terminals can support the execution of powerful cryptographic security algorithms for financial transactions

The term “cryptocurrency” has been coined, and is being used as in Section 3, to indicate that these instruments are cryptographically secured “digital” entities. They are encrypted numbers with assured digital signature authenticity. Such systems provide algorithms for minting and managing the coins. The present-day milieu of cryptocurrencies, parallels the days of the original gold rush. The computational mechanisms behind the cryptocurrencies are sound – mathematical proofs-of-work set the standards for minting new coins, transaction fees and distributed maintenance structures. On the other hand, the usage of some private or cryptocurrencies for certain contraband goods and services together with the  floating value of the currency based on market forces prevent the widespread acceptance of such currencies.

An important facet of physical money is social equity. Physical cash instruments sanctfied by the state are universally accepted store-of-value. The physical coins can be held and exchanged by any individual irrespective of any societal standing of the individual.

The mobile phone penetration into the society is almost complete. Today, there are certain forms of “electronic” money systems managed by some telecom and banking service providers. All of these are offered as prepaid value added services. Indeed the talk-time paid for by an user to a telecom service provider is called “currency”. Such systems have limited clientele and work in a cartel of service providers and merchants. These systems do not provide for the full range of financial, banking and micro-finance operations (deposits, loans, insurance, subsidies and wages) that can be conducted through cash, for legitimate activities, in organized and informal systems. Also the principle of financial inclusion” is to enable and empower every citizen to take advantage of all these financial products and services.

The technological enablers of a digital economy such as mobile phones and similar low-cost devices such as tablet computers and point-of-sale (POS) terminals can support the execution of powerful cryptographic security algorithms for financial transactions. In short we get our money’s worth of computations! It is only required to design and adopt a suitable currency or monetary system to work with these technological devices.

Hence we introduce a virtual money which will be a digital vehicle for conducting financial transactions and provide for all the products and services under the umbrella of financial inclusion. This is described briefly in Section 4.5. Before describing our virtual money proposal we discuss the salient statistical and economics aspects of fiat money.

4.2 Cash Statistics

 There are several advantages of the instrument of physical money (cash) over conventional alternatives based on the media of paper, plastic and electronic advice (internet, mobile banking). These properties of cash include: divisibility, fluidity, privacy, peer-to-peer immediate-settlement. More importantly, the instrument of physical cash provides for the handling of a large number of small value transactions. This is in contrast with the case of a small number of large value transactions. The graph of the number of transactions (y-axis) versus the value of the transactions (x-axis) would follow the power-law distribution (y ≃ x^-α with α > 1) and will have a long tail. Such distributions are typical characteristics of many socio-economic phenomena.

In order to understand the role of a fiscal instrument in the economy, it is important to analyse the transactional properties. In an ongoing work we study these in detail in the Indian and global contexts. We give a rough indication here. Assuming a geometric mean of 20 cash transactions per day per household of value of Rs 10 each, and 200 million house-hold consumers the cash in circulation per year is about Rs 14 trillion, or about 10% of the GDP of the country. This value tallies with the value of cash in circulation according to a recent RBI statistical report! Further, this proportion of cashin- circulation economic indicator is in consonance with the global figures in the range of 5% to 15% for different countries. To complete the picture of the use of cash we provide next a simple analysis of income and spending.

4.3 Wages and Spending Statistics

 We discussed cash in circulation. Now, we complete the book-keeping China is seeking to ban cryptocurrencies and, India  is considering state issued fiscal cryptocurrencies. The full definition of such a fiat cryptocurrency are not yet availabe. primarily a digital, fiat currency instrument in the cryptocurrency genre will have the following features by making estimates on wages and deduce spending patterns. A first-cut simplified model and graph of earnings is as follows. Assume a 16 wage pattern of Rs.2⁸ to Rs.2²³ on the x-axis. Assume a 16 step grouping of wage earning population ins sizes of 2¹¹ to 2²⁶ on the y-axis. We consider the scale log₂. Now a simple log-linear graph with a negative slope of -1, depicts the reciprocal power law y ≃ x^-1. For example, the left-most point (8, 26) says that there are 64 million people earning Rs.256 per day, near the statutory minimum wage. The right-most point (23, 11) says that there are 2048 people earning Rs. 8 million per day! With these, we get that the total earning per year is ≃ 256 * 16 * 2³⁴ = 2⁴⁶ â‰ƒ Rs. 64 trillion, a reasonable fraction (0.46) of the GDP of India.

This model gives us a handle on a rational model for spending, which is related to the use of a fiscal instrument. The average numbers, sizes and the types of instruments used for spending are correlated with the composition of the population based on their earning capacities. From the simple model for earning discussed above, we deduce that the cash based transactional operations will roughly follow the assumptions of Section 4.2, namely, 2 billion transactions of about Rs. 20 per day! Note that the total earning at the lowest daily wage earning population of Rs.234 (or about Rs. 16 trillion) roughly equals this amount. This rightly means there can be no saving at this level! Indeed the savings are generated by higher levels of earnings. This is also consistent with economic data on national savings. It is possible to carry out more fine calculations to determine the quantum of micro savings and consequently the micro-investments possible.

4.4 Digital Fiat Currency

 The rise of Bitcoin and a few other cryptocurrencies in a short span of time has stirred the creative, pecuniary instincts of many digital entrepreneurs. A large number of cryptocurrencies have bloomed. Many of these will be shortlived, as the digital firms spawning these will themselves fold and disappear or get absorbed into or acquired by merged with firmer companies. Also the governments of many countries are becoming more concerned with the phenomenon of cryptocurrencies on two counts: (i) the financial volatility of the cryptocurrency stock and hence the consequential issues of investment regulations and civil law and order, and (ii) the distributed, ephemeral geotemporal transactional boundaries and hence the consequential issues of geopolitical control and governance.

Ironically, in recent moves, China is seeking to ban cryptocurrencies and, India is considering state issued fiscal cryptocurrencies [9]. The full definition of such a fiat cryptocurrency are not yet available. Primarily a digital,  at currency instrument in the cryptocurrency genre will have the following features. We list these along with brief descriptions.

1. blockchain information structures – adopted in the form of pre-defined stacks (or bundles) of one-way linked chains of digital descriptors maintained in publicly verifiable ledgers. The volumes will be based on monetary, financial and technological considerations.

2. unique identification – will be provided by means of hash-chains and digital signatures.

3. store-of-value – will be governed by issuance regulations and documented in the digital data structures.

4. medium-of-exchange – will be governed by provenance and exchange regulations, documented in the data structures and verified on the network.

5. transfer, double-spending controls – will be handled by sophisticated cryptographic algorithms and operational regulations.

6. transactions and proof-of-work – will be categorized based on the value of transaction, into a graded system of large to small values and an associated scheme of proportional proof-of-work-computations.

7. transaction logs – will be maintained and handled by the state through its network of trusted institutions such as banks.

It can be seen from the above properties that some of these are departures from the prevalent notions of fully distributed schemes of operations. However, even the prevalent cryptocurrencies are tending to be non-egalitarian in that the corporate, first-mover, market-capture advantage has come to stay because of the investment for the computational resources required for minting and establishing proof-of-work.

A system developed by us called VSKchains, [30] includes a cryptocurrency termed VMcoins that has all of the desirable properties required by the state. It is semi-distributed with certain types of central operational controls. It has many monetary, economic, and financial provisions of benefit for both the citizen and the state, such as direct benefit transfer, micro-finance and taxation.

4.5 Our Money

 Our proposal of a virtual money (VM) based on the instrument of “VMcoin” uses the cryptographic mechanisms of hashing, encryption and digital signatures. We differ from the Bitcoin type of cryptocurrency, in that we adhere strictly to the standards of denominational fiat currency and mimic exactly the instrument of state supported physical cash. The principal novelty is that our virtual money goes mobile! The VMcoins will be held in VMwallets in mobile phones. Transactions between mobile phone VMwallets will be enabled by a system of electronic exchange schemes (NFC, Bluetooth, WiFi, QRcode scans) and backend coin database updates.

4.5.1 VSK Chains and VM Coins

 As mentioned above, our conceptual design of new semi-centralized blockchain architecture to facilitate both monetary and content transactions called the VSKchains is given in [30]. We also introduced a central coin issuing authority (CIA) who issues and manages coins. The system VSKchains consists of two parts: (i) the transactional information pertaining to the content of an application, and (ii) the payment or monetary information pertaining to this transaction. We call the associated chains of blocks of information or structured data as: (i) chains of blocks of content transaction chains, denoted BS, and (ii) chains of blocks of monetary transaction chains, denoted BM. A pair of entities are involved in any transaction of the chains. They are referred to by paired terms such as payer-payee, sender-receiver, prover-verifier etc. The Figure 3 is the conceptual design of VSKchains.

Here, a central Coin Issuing Authority (CIA) issues a digitally signed stack of coins. Each coin will have a fixed denomination or token value. Each content or monetary transaction contains transaction ID T, sender X and receiver Y information, content C. The transaction is also linked to other related transactions within and across content and monetary transaction chains. The Figure 3 illustrates the  flow of information. It also indicates (i) hc, hs representing the input, output hash values, (ii) fl, bl representing forward and backward links for search purposes. The format of ith coin is

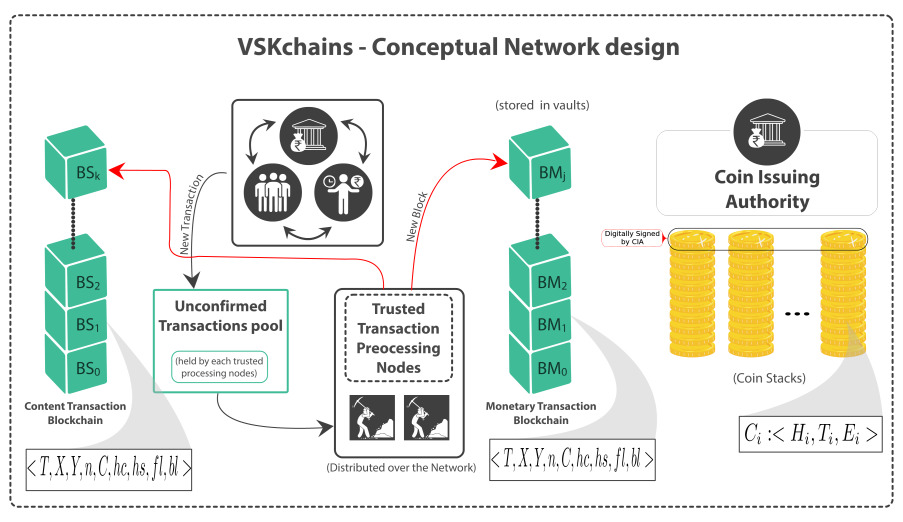
Figure 3: VSKchains – a Conceptual Design

Ci = <h_{i, Ti,Ei>, where Hi, Ti,Ei, denoting the head, tail and edge of the coin Ci, contain information such as denomination, coin id, previous, current owner IDs, number of spendings of Ci, and place and time of transactions. All the transactions are processed by trusted hierarchical system of nodes distributed over a network. These nodes also verify the integrity of coins and check for double spending. Further details about the architecture and algorithms which use information structure can be found in [30] In this work, we also introduce a new hash function [28] , [29] to perform transaction hashing, block hashing and coin generation.</h}

We have implemented a proof-of-concept version of the financial transaction aspect of the VSKchains system. We have also built a simulator for generating statistics of real-world systems of financial transactions. With these attempts, we claim that the novelty of our proposed VSKchains system consists in its ability to provide both transactional features and man financial inclusion related features, discussed in Section 4.1.

crytography offers the theory of one-way functions that can be computed easily in the forward direction, typically from a discrete domain set to a discrete range set, but are difficult to compute in the reverse direction 

4.6 Proof-of-work, Cryptographic Hash Functions

All blockchains and cryptocurrencies use a proof-of-work construct to establish, unequivocally and in a verifiable manner the claim-to-priority or ownership of a digital record. The nature of the construct is such that the computational effort needed to establish the proof can be precisely quantified based on the state-of-science of the candidate mathematical problem.

Cryptography offers the theory of one-way functions that can be computed easily in the forward direction, typically from a discrete domain set to a discrete range set, but are difficult to compute in the reverse direction. The term easy means that the computational effort is polynomially bounded in the length of the input, and the term difficult means that the computational effort is not known to be polynomially bounded in the length of the input. For example, all cryptographic hash functions, such as MD5, SHA family, RIPEMD, are of this kind. Formally, H : D = {0, 1}ⁿ => R = {0, 1}²⁵⁶, denotes a hash function which maps binary strings x of length n to a binary string y of length 256 bits. The design of cryptographic hash functions H draws upon, the principles of design of block ciphers, which carry out several rounds of specific substitution, and permutation operations on the input string, thereby achieving a randomization of the input. Further, empirical guarantees are provided that:

(i) computing y = H(x) is polynomially bound in the length |x| of x
(ii) solving any of the following three problems is hard

1. find x₁, x₂ such that y = H(x₁) = H(x₂), (termed find collision)
2. given y (= H(x)), find x = H^-1(y), (termed, find pre-image)
3. given x₁, y with y = H(x₁), find x₂ = H^-1(y), (termed find second
pre-image)

For well-designed cryptographic hash functions the three problems are, apparently, of the same degree of difficulty. There is a subtle gradation of the difficulty level – they are of increasing hardness from the first to the third. In general, it is believed that the difficulty level is exponential in the input length. This tenet is the basis for the design of proof-of-work constructs (see Section 3.2.1, items 5-7).

A typical proof-of-work mechanism used in blockchains and cryptocurrency is as follows. The scenarios consist of a prover (responder) P and a verifier (challenger) V . The challenger (or verfier) V gives the prover P an initial string x, a specific target string y, and asks P to find a nonce (number once) N such that H(x + N) = y. Here H is typically a 256-bit hash function. This problem is equivalent to finding a pre-image, and the computational effort is expected to be exponential in the length of the specified the string. A typical string y is of the form < 0,.., 0, b_k+1, … , b₂₅₆ >, i.e., a binary string in which the fi rst k bits are set to 0 and the remaining 256 – k bits are free. The expected effort is 2k hash computations since the only known way of obtaining N seems to be to run through all 1 ≤ i ≤ N. Values of k >40 require tera-scale hash computations per second and set the computing requirements manageable by only large enterprises. Note that the current difficulty levels in Bitcoin is equivalent to k ≃ 63, as shown above.

There are various choices and considerations in the use of hash functions for proof-of-work computations. We list these issues.

1. functions: SHA-256, scrypt, custom hash algorithms used in Bitcoin, Litecoin and others, respectively.

2. performance: software, special and general purpose hardware – PC clusters, FPGA, GPU and accelerators.

3. time-memory tradeoff: scrypt algorithm provides such a feature which is important as it becomes harder to mint new coins.

4. hashes per second: typical software benchmark figures vary from 1 million to 10 million hashes per second on standard PC platforms. The industry has advanced to much higher levels of optimization and enhancement for specific applications using custom hardware and software.

Cryptocurrencies, require an act of minting newer and a limited number of coins. The first finder gets a reward. Hence a proof-of-work is a natural requirement. Clearly, the proof-of-work phenomenon is an overkill for all kinds of blockchain applications.

We introduce a new paradigm, of graded proof-of-work, suitable for a variety of blockchain applications. The proof-of-work demanded of the prover, can be made arbitrarily light or heavy. This can be designed based on one of the following three principles:

(a) effort polynomial in input size
(b) effort sub-exponential in input size
(c) effort exponential in input size.

Further, the three schemes can include a linear scaling parameter, such as an iteration count, to amplify the effort to match the desired work factor. Thus the effort for the generation of proof-of-work can be made light-weight to medium-weight to heavy-weight, depending upon the demands of the application. Our proposal above is suitable for many different scenarios, varying from straight-forward and routine blockchain applications, such as university transcript management information systems (light-weight), to patient-record MIS (medium-weight) to banking and financial MIS (heavy-weight). Variations on this theme, are the permissioned-blockchains discussed in [31].

The Blockchain Technology is also expected to improve information processing performance. Hence many of industries are adapting this technology as private or permissioned Blockchains.

5. Future of Blockchains and Cryptocurren-cies

 Technology, like fashion, also goes through a social cycle. Often it reinvents itself during historical epochs. The beginning of a transitional periods is beset with many uncertainties such as cost-benefit ratios, acceptability, reliability, robustness. The phenomena of cryptocurrencies and blockchains are undergoing such initial troubles. We discuss some issues and propose modest directions.

5.1 Blockchains

 The Blockchain technology gained prominence with the introduction of the Bitcoin. This has found many other applications in recent years. The Blockchain technology is a trusted, decentralized, public ledger system. This technology provides a solution to a vexing problem in distributed computing called the Byzantine Generals Problem or fault tolerance problem. Hence, the Blockchain technology is expected to have many applications in distributed computing including Internet-of-Things.

A recent report by the technology consulting company, Gartner, underscores such concerns under the catchy phrase “blockchains – hope or hype” and tends to indicate that the blockchains notion has crossed the initial, peak hype levels and is perhaps maturing. Many applications in the nature of management information systems (IS), enterprise resource planning (ERP), e-commerce, e-governance, internet-of-things and others are being vigorously, re-examined in the setting of secure, transparent, distributed ledgers of blockchains. The global electronic connectivity is getting better. As a consequence there is a shrinking of the digital world of information transactions and fiduciary transactions. These portend many benefits from the adoption of blockchain technology, in almost every aspect of information technology including cloud, and IoT systems.

5.2 Cryptocurrencies

 The blockchain technology of cryptocurrencies is based on strong technological foundations. On the other hand the matters of their use, management benefits are, in general, unclear. Some of these are contentious between the citizen, the business and the government. We provide two technical directions for further work. The first one is applicable equally to general blockchains.

5.2.1 Useful Proof-of-Work

 Research investigations in which the straight-forward, exhaustive enumeration based computations to reach a specific hash value can be made more useful. The intermediate computations leading to the final values will be useful, if these values have a scientifically useful semantics – for example, they could correspond to the search for difficult-to-find numbers or combinatorial objects. Many mathematical problems requiring certain amount of empirical data to support the purely theoretical deductions can serve as candidate proof-of-work problems.

5.3 Hybrid Cryptocurrency Schemes

 The Blockchain Technology is also expected to improve information processing performance. Hence many of the industries are adapting this technology as private or permissioned Blockchains (e.g., ntech/central banking, consortium of private industries in supply-chain management).

We have argued in favor of a semi-centralized or quasi-distributed blockchain based cryptocurrency and provided a new design Section(4.5). Our proposal strikes a balance between completely distributed versus the completely centralized versions of blockchains. Distributed systems offer the advantages of speed and fault tolerance, but need to contend with synchronization and security issues. Centralized systems, in general, have to work hard to provide performance and reliability guarantees, but can easily manage consistency and security issues. A combination of both philosophies, in the form of hybrid systems that provide good transaction handling capabilities with trusted payment features, is more likely to score over either approach used separately. We note that such a hybrid view has supporters. It also has detractors, the notable person being the well-known open blockchain evangelist Antonopoulos. The commentaries of these people appear often in the trade and web literature. However, the consulting firm Deloitte has come out with a report [14] on the viability of a state sponsored fiat cryptocurrency that would combine the merits of a fiat currency with those of a cryptocurrency.

6. Conclusions

 We have given an expository description of the topic of cryptocurrencies. We have provided an analytic view of various interconnected issues, drawing upon tenets from cryptography, digital cash, cryptocurrencies, blockchains and socio-economics of money. There has been a spurt in trading and commercial activities generated by active financial technology entrepreneurs, beginning with the Bitcoin system and a large number alternative cryptocurrencies, in a short span of time. This has led to concerns among government, corporate and academic sectors about different aspects of the phenomenon of and discussions in many fora. We have attempted to cover these issues in a critical manner so as to provide a basis for future studies.

A The ECDSA

 The Bitcoin network uses the elliptic curve digital signature algorithm (ECDSA) for purposes of claiming ownership and transfer of a bitcoin by a user. In this section we describe briefly the ECDSA. The ECDSA consist of a pair of keys called public and private keys. A public key is derived from a suitably chosen private key. It is computationally difficult to recover the private key from the public key. This setup gives a cryptographic one-way function used in public key cryptography for various information security functionalities. For more details about the elliptic curves in cryptography refer [6] , [7] , [17].

The general equation of an elliptic curve over a field F is given by the equation

Є : Y ² + a₁XY + a₃Y = X³ + a₂X² + a₄X + a₆, a_i Ð„ F        (1)

denoted by f(X, Y ) or Є.

An elliptic curve over a field F, denoted by Є(F), is the set of solutions in F×F satisfying the equation of the form (1) along with a point at infinity denoted by O.

If the characteristic p of F is greater than 3, then the equation (1) reduces (by simple squaring and cubing appropriate terms) to

Y ² = X³ + aX + b a, b Є F      (2)

with the discriminant of the equation Δ = -16(4a³+27b³) ≠ 0 (which follows from non-singularity of E). This is same as the condition that the right side of the equation (2) should not have multiple roots.

A.1 Group Law

 An elliptic curve E(F) forms an additive abelian group with respect to chord-tangent law, with the point O as identity element.

For prime p > 3, the addition of two points P = (x₁,y₁) and Q = (x₂, y₂) over Є, given in terms of affine co-ordinates, is as follows. Let P+Q = (x₃, y₃)

and P ≠ Q, then
 
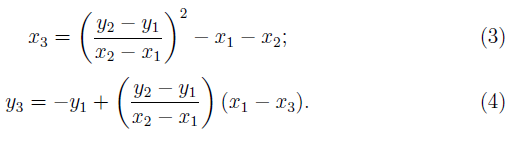
If P = Q, then
 
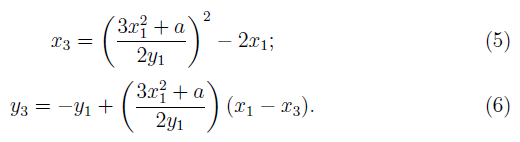
Note that -P = (x, -y) if P = (x, y).

It is easy to compute Q = nP for given P and n using the double-and- add algorithm. But the converse is computationally difficult. The discrete logarithm problem over an elliptic curve Є(ECDLP) defined over a finite field Fq is that of computing an integer n > 0 (if exists), such that Q = nP for given P, Q in E(F_q). The computational complexity of solving the ECDLP is basis for many public key cryptosystems.

A.2 Description of the ECDSA

 The digital signature is used to establish the integrity, authenticity and nonrepudiability of signing of digital documents. Well-known digital signature schemes, that are included in several standards like NIST, are The Digital Signature Algorithm (DSA) defined over a finite field and the Elliptic Curve Digital Signature Algorithm (ECDSA) over an elliptic curve. The Bitcoin network uses the ECDSA.

Let user A sign a digital document M that can be verified by anyone. User A chooses a cryptographically secure prime p, an elliptic curve E, with a base point P of order N. A chooses an integer d Є_R [1,N – 1] randomly, and computes Q = d P (scalar n multiple of P). A keeps d secret and makes (p,Є,N, P,Q) public.

To sign a message M, A will do the following.

1. Compute e = h(M) (hash of the message M and with e < N as an
integer)

2. Choose k Є_R [1,N – 1] (using a cryptographically secure PRNG)

3. Compute (x1, y1) = k P, and r = X1 (mod N)

4. Compute s such that k s = e + r d (mod N)

Then the pair (r, s) is signature on M by A.

Any third party can verify the signature as follows.

1. Compute e = h(M)

2. Compute w = s^-1 (mod N)

3. Compute (x, y) = we P + wr Q

4. Signature is valid if r ≡ x (mod N)

For further details on the parameters : prime, elliptic curve, and the base point refer to NIST standard document [16]. A bitcoin address is derived from the public key of a user using a hash function. Since public and private keys are uniquely associated, a bitcoin address is thus uniquely associated with the private key, hence represents the user uniquely.

A.3 Curve used in Bitcoin network

The Bitcoin network uses an elliptic curve secp256k1 suggested by the NIST standard. The elliptic curve defined in secp256k1 is y² = x³+7 over F_p where p is a 256 bit prime given by p = 2²⁵⁶ – 2³² – 2⁹ – 2⁸ – 2⁷ – 2⁶ – 2⁴ – 1.

References

 
[1]M. Abe and E. Fujisaki, “How to Date Blind Signatures”, Advances in Cryptology – ASIACRYPT ’96, LNCS, Volume 1163.

[2] R. Anderson, C. Manifavas and C. Sutherland, “Netcard – a practical
electronic cash system “, Fourth Cambridge Workshop on Security Protocols, LNCS, April 1996.

[3] Andreas M. Antonopoulos, “Mastering Bitcoin – Programming the Open Blockchain, O’Reilly Media, Inc., 2017.

[4] Adam Back, “Hashcash – A Denial of Service Counter-Measure, 2002.

[5] E. Ben-Sasson, A. Chiesa, C. Garman, M. Green, I. Miers, E. Tromer,
and M. Virza, “Zerocash: Decentralized Anonymous Payments from Bit-coin”, 35th IEEE Symposium on Security and Privacy, 2014.

[6] Ian F. Blake, and Gadiel Seroussi and Nigel P. Smart, “Elliptic Curves in Cryptography”, London Mathematical Society, Lecture Note Series 265, Cambridge University Press, Cambridge, 1999.

[7] Ian F. Blake and Gadiel Seroussi and Nigel Smart, “Advances in Elliptic Curve Cryptography”, London Mathematical Society, Lecture Note Series 317, Cambridge University Press, 2005.

[8] S. Brands, “Electronic Cash on the Internet” , Proceedings of the Internet Society 1995 Symposium on Network and Distributed System Security, February 1995.

[9] Business Standard, “Govt considering its own cryptocurrency”, 16 Sept 2017, http://www.business-standard.com/article/economy-policy/govtconsidering-its-own-cryptocurrency-117091600051 1.html

[10] D. Chaum, A. Fiat and M. Naor, “Untraceable Electronic Cash”, Advances in Cryptology – CRYPTO’88, LNCS, Volume 403, 1990.

[11] D. Chaum, “Blind Signatures for Untraceable Payments”, Advances in Cryptology – Crypto ’82 Proceedings, Plenum Press, 1983.

[12] D. Chaum, “Security without Identication: Transaction Systems to Make Big Brother Obsolete”, Communications of the ACM v.28, no.10, October 1985.

[13] K. Croman, C. Decker, I. Eyal, A. E. Gencer, A. Juels, A. E. Kosba, A. Miller, P. Saxena, E. Shi, E. Gun Sirer, D. Xiaodong Song and R. Wattenhofer, “On Scaling Decentralized Blockchains – (A Position Paper)”, Workshop on Bitcoin Research (BITCOIN 2016).

[14] Deloitte Report, “State-Sponsored Cryptocurrency”, 2015, https://www2.deloitte.com/content/dam/Deloitte/us/Documents/strategy/uscons- state-sponsored-cryptocurrency.pdf

[15] C. Dwork and M. Naor, “Pricing via Processing or Combatting Junk Mail”, Advances in Cryptology – CRYPTO’ 92, LNCS, 1992, Springer Berlin Heidelberg, pp 139{147.

[16] FIPS PUB 186-4, “Digital Signature Standard (DSS)”, National Institute of Standards and Technology, Gaithersburg, July 2013.

[17] Darrel Hankerson, Alfred J. Menezes, Scott Vanstone., “Guide to Elliptic Curve Cryptography”. Springer Professional Computing. Springer, New York, 2004.

[18] R. Hauser, M. Steiner and M. Waidner, “MicroPayments based on iKP Technical report”, IBM Research Division, Zurich Research Laboratory, January, 1996.

[19] The Hyperledger Project, A Blockchain Technologies For Business, https://www.hyperledger.org/

[20] Y. Lewenberg, Y. Sompolinsky, A. Zohar, “Inclusive Block Chain Proto-cols”, Financial Cryptography and Data Security, FC 2015, LNCS, vol 8975. Springer, 2015.

[21] G. Medvinsky and B.C. Neumann, “NetCash: A design for practical electronic currency on the Internet”, First ACM Conference on Computer and Communication Security, November 1993.

[22] Satoshi Nakamoto, “Bitcoin: A Peer-to-Peer Electronic Cash System”, www.bitcoin.org, 2008, https://bitcoin.org/en/bitcoin-paper.

[23] D. Pointcheval and J. Stern, “Provably Secure Blind Signature Schemes”, Advances in Cryptology – ASIACRYPT ’96, LNCS, Volume 1163.

[24] R.L. Rivest and A. Shamir, “PayWord and Micromint – Two simple Micropayment Schemes “, preprint, MIT, May 1996.

[25] R.L. Rivest, “Electronic Lottery Tickets as Micropayments”, preprint, MIT.

[26] R.Saianand and C.E.Veni Madhavan, “An Online Transferable, E-cash Payment System”, Progress in Cryptology – INDOCRYPT 2000, LNCS Vol 1977, Springer, Berlin, pp.93-103.

[27] SAHASRAT, India’s First Petascale System, http://www.serc.iisc.in/facilities/cray-xc40-named-as-sahasrat/

[28] Ch. Srikanth, “Computational and Number Theoretic Aspects of Certain Collections of Arithmetic Progressions”, Phd Thesis, Indian Institute of Science, 2017.

[29] Ch. Srikanth, C.E. Veni Madhavan and H.V. Kumar Swamy, “Family of PRGs based on Collections of Arithmetic Progressions”, Cryptology ePrint Archive, Report 2017/324, 2017, http://eprint.iacr.org/2017/324.

[30] C.E.Veni Madhavan, Ch. Srikanth and H.V.Kumar Swamy, “VSK Chains: Integrated Content and Currency Transaction Blockchains”, International Conference on Advanced Computing and Communications (ADCOM), 2017.

[31] Marko Vukolic, “Rethinking Permissioned Blockchains”, Proceedings of the ACM Workshop on Blockchain, Cryptocurrencies and Smart Contracts, BCC ’17, 2017.

[32] Zcash, https://z.cash/, (a improved version of Zerocoin based on zeroknowledge succinct non-interactive adaptive argument of knowledge
(zkSNARK)).